この記事では断面二次半径について書いていきます。
断面二次半径は座屈計算をするときに必要な値です。断面二次モーメントを断面積で割った値の平方根をとったものが断面二次半径となります。実際の長方形断面や円形断面での求め方を紹介していきましょう。
目次
断面二次半径とは?求め方は?
早速断面二次半径の公式を紹介しましょう。
k = √ ( I / A)
(k:断面二次半径[mm]、I:断面二次モーメント[mm⁴]、A:断面積[mm²])
こちらが断面二次半径の公式となります。断面二次半径の単位は、[mm]です。長さの4乗([mm⁴])である断面二次モーメントを、断面積[mm²]で割り、さらに平方根を取っているため、断面二次半径の単位は[mm]となります。
断面二次半径は主に座屈計算をするときに使われる物理量です。座屈計算をするときは、オイラーの式やランキンの式を使いますが、ここでオイラーの座屈応力の計算式を見てみましょう。
σ = n × π²E/λ²
(σ:座屈応力[MPa]、n:断末係数、E:縦弾性係数(ヤング率)[GPa]、λ:細長比(=l/k))
座屈応力を求めるときの計算式の分母に細長比のλが入っていますが、細長比λは柱の長さlを断面二次半径kで割った値です。この細長比λを計算するときに断面二次半径kは使われます。
断面二次半径の求め方
では実際に求め方を紹介していきましょう。円形断面と長方形断面の場合の断面二次半径の求め方についてです。
中実円形断面の断面二次半径
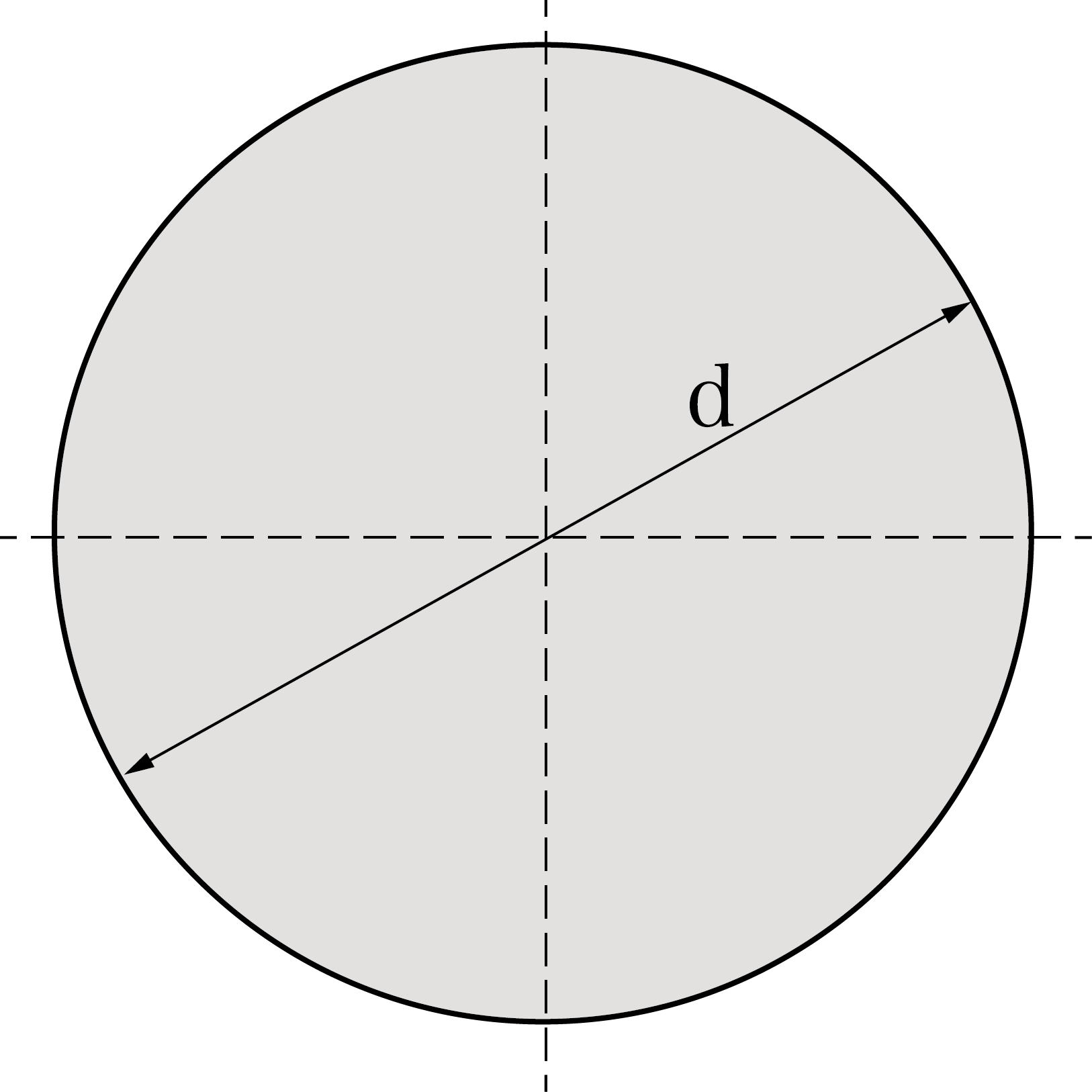
最初に中実円形断面の断面二次半径を計算していきましょう。断面二次半径kを求めるためには断面二次モーメントIと断面積Aが必要なのでしたね。ということでまず断面二次モーメントと断面積から求めます。
断面二次モーメントI = πd⁴/64、断面積A = π(d/2)² = πd²/4
断面二次半径kは断面二次モーメントIを断面積Aで割った値の平方根をとったものですので、
断面二次半径k = √(I/A) = √(πd⁴/64 × 4/πd²) = √(d²/16) = d/4
こちらが中実円形断面の断面二次半径です。
中空円形断面の断面二次半径
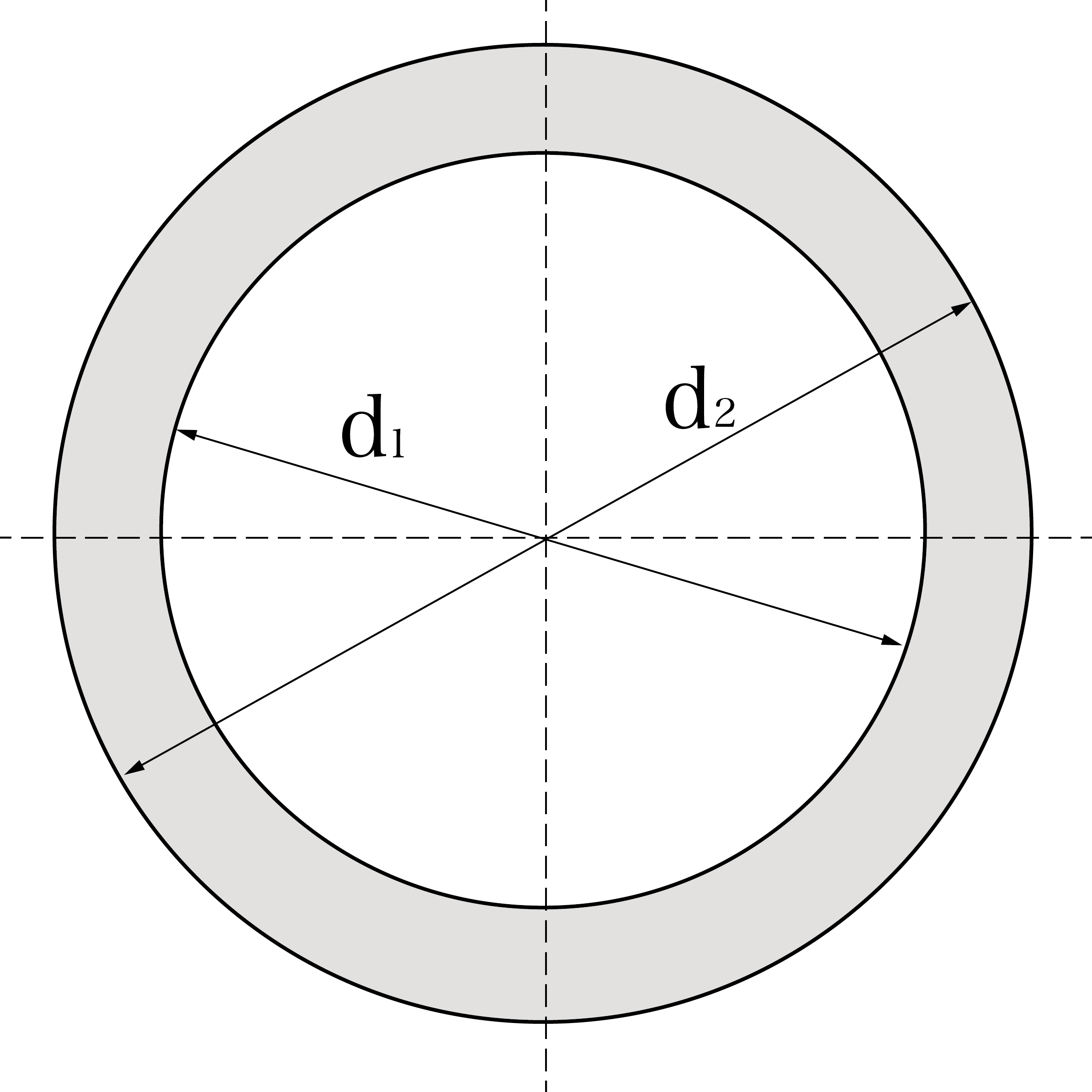
中実円形断面と同様に、中空円形断面の断面二次半径を求めていきます。
断面二次モーメントI = π(d2⁴-d1⁴)/64、断面積A = π(d2²-d1²)/2² = π(d2²-d1²)/4
断面二次半径k = √(I/A) = √{π(d2⁴-d1⁴)/64 × 4/π(d2²-d1²)} = √{(d2²+d1²)(d2²-d1²)/16(d2²-d1²)} = √(d2²+d1²)/4
こちらが中空円形断面の断面二次半径です。
長方形断面の断面二次半径
次長方形断面の断面二次半径です。長方形断面は、横長の場合と縦長の場合で断面二次モーメントが異なるので、断面二次半径も違った値をとります。実際に横長長方形断面の断面二次半径と、縦長長方形断面の断面二次半径を計算して違う値をとることを確認しましょう。最初は文字のまま計算をし、縦長と横長の値の比較は値の代入時に検証します。
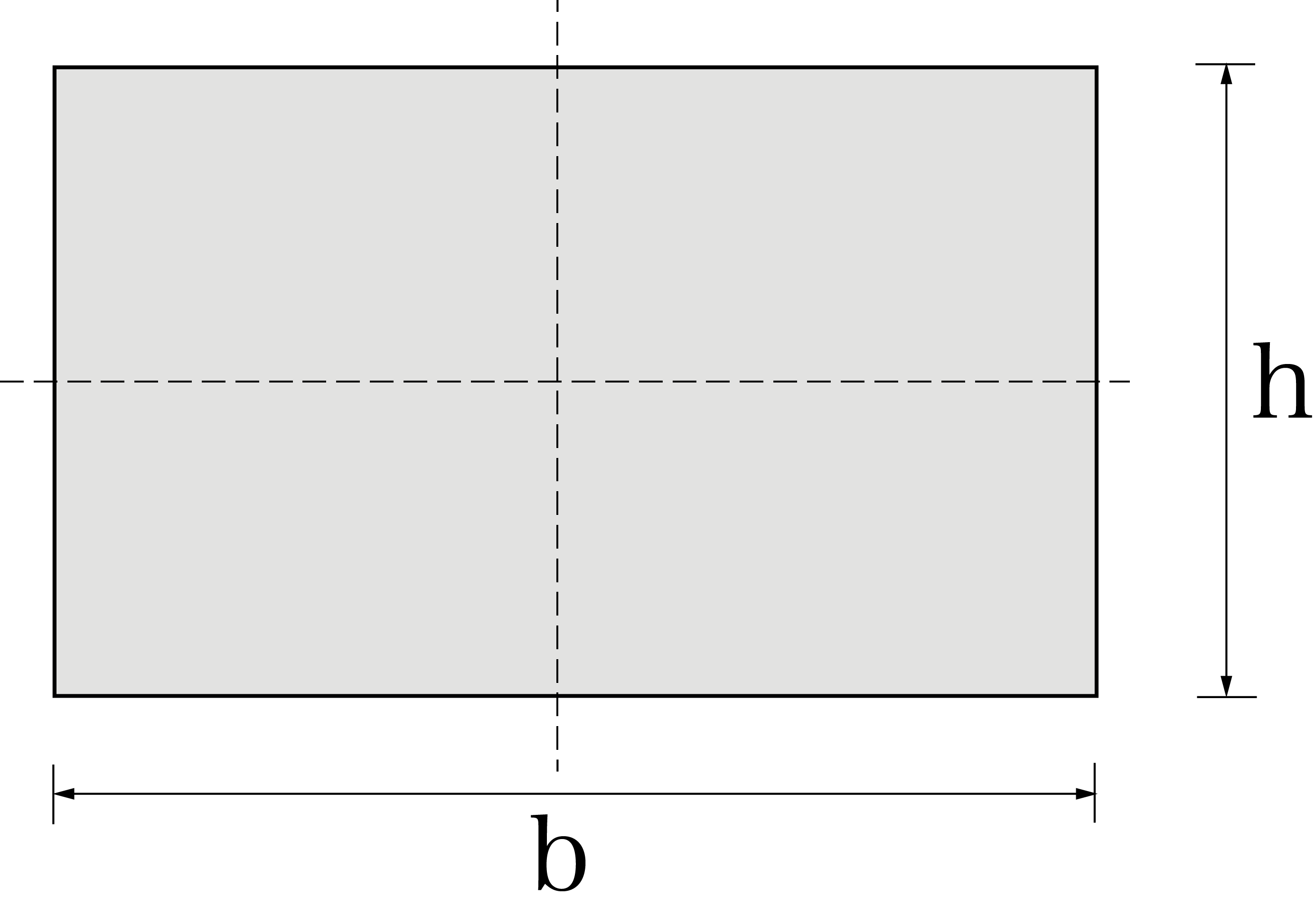
bを横の辺、hを縦の辺とします。
断面二次モーメントI = bh³/12、断面積A = bh
断面二次半径k = √(I/A) = √{(bh³/12)/bh} = √(h²/12)
横長長方形断面の場合
横長長方形断面の場合b>hなので、上の図の通りとなります。よって、
横長長方形断面の断面二次半径k = √(h²/12)
縦長長方形断面の場合
横長長方形断面の場合b<hとなります。よって、短い辺がbとなるので、下のようになります。
横長長方形断面の断面二次半径k = √(b²/12)
長方形断面の断面二次半径は、基本的に短い辺を代入して計算をするだけです。短い辺を代入する=最小断面二次半径を求めるということですので、断面二次半径は常に小さくなる値を考えましょう。
円形断面の場合はどこでも直径が一緒ですので、どの直径の値を代入しても断面二次半径の値は一定ですが、長方形断面の場合は代入する値が変わると断面二次半径の値が変わります。このことも合わせて覚えておきましょう。
まとめ
今回は断面二次半径の公式と、いろいろな断面の断面二次半径の計算の仕方を紹介しました。全部を一気に覚えていきなり計算をしていくのは難しいと思うので、断面二次半径を求めるときはこの記事を参考にしながら計算をしていくと良いでしょう。
今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。



とてもわかりやすかったです。本当に助かりました!