柱の座屈計算(オイラーの式・ランキンの式)手順まとめ

この記事では比較的難しい座屈計算の手順を紹介していきます。この記事を読んで理解すれば、座屈計算を完璧にすることができます。ぜひマスターして今後の勉強に役立ててくださいね。座屈計算は覚えることが少々ありますが、解放の手順を整理して明確に計算をして生きましょう。

 

短柱・中間柱・長柱の座屈現象ついて

まず初めに座屈現象はどのような柱に発生するものなのかを解説して生きます。。

柱は短柱・中間柱・長柱の3つに分類されます。短柱は座屈は生じない柱です。そのため圧縮荷重が作用した場合でも垂直応力を計算しますので、座屈現象は関係ありません。

残りの2つである中間柱と長柱で座屈現象は生じます。逆にいうと、座屈が生じる柱を中間柱と長柱としています。

中間柱と長柱で座屈荷重・座屈応力の計算式が違います。中間柱のときはランキンの式、長柱のときはオイラーの式で計算します。

ランキンの式、オイラーの式の詳しい計算式については以前まとめたものがありますから、そちらを参照してください。

ランキンの式まとめ！座屈定数や長柱・中間柱の決定方法

座屈とオイラーの式について！座屈応力と座屈荷重の計算方法

 

さて、では実際に例題を見ながら座屈計算である座屈応力の計算手順を見ていきます。

 

座屈計算手順を例題で確認しよう

では実際に例題を見ながら手順を説明していきます。

長さ1[m]、断面寸法80[mm]×38[mm]で両端を固定した軟鋼性の柱の座屈応力を求めなさい。縦弾性係数(ヤング率)を206[GPa]とします。

 

手順1：断面二次半径kを求める

最初に柱の断面二次半径を求めます。「柱が中間柱と長柱では計算式が異なるからまずは計算式を決めるんじゃないの？」と思うかもしれません。しかし、座屈計算をするランキンのしきもオイラーの式も、どちらも断面二次半径kと細長比λを使います。そのため、これらを先に求めて、実際に座屈応力を計算するときにどちらの式を使うか決定しましょう。

断面二次半径は、断面二次モーメントを断面積で割った値の平方根をとったものです。

今回の例題の断面積A=bh、断面二次モーメントI=bh³として、

断面二次半径k = √(I/A) = √(bh³/12bh) = √(h²/12)[mm]

ここでは文字のまま進めていきましょう。

 

手順2：細長比λを求める

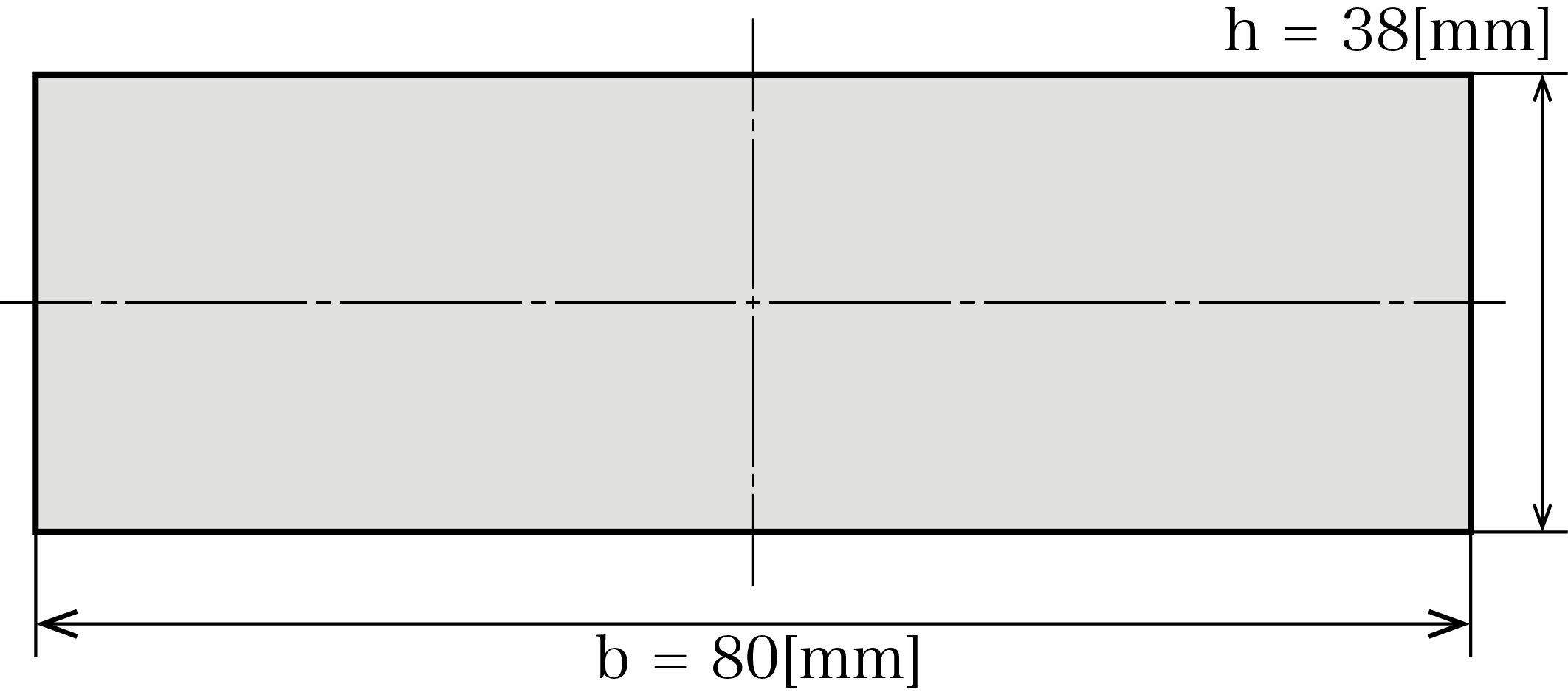
断面二次半径の次に、細長比λを求めます。例題の断面は上の図のようなものでした。

細長比λ = l/k = l/√(h²/12) = 1,000/√(38²/12) = 91.2

上の計算式のhには、断面の短い方の辺である38[mm]が代入されています。座屈は最小断面半径で計算しますから、値が小さくなるような辺の長さを代入しています。細長比は文字通り”比”ですので、単位はありません。

 

手順3：計算式の決定

ここの手順がなかなかつまづく人が多いです。しかし整理していけば簡単ですので、身構えずに読んでいってください。

座屈の計算は、柱が中間柱か長柱かで計算式が異なるのでしたね。中間柱のときはランキンの式、長柱のときはオイラーの式で計算します。

中間柱か長柱の選定方法ですが、柱の素材によって異なってきます。今回の例題の柱は軟鋼製ですので、λ<90√nを満たしていれば中間柱で計算式はランキンの式になります。そうでない場合(λ>90√n)の場合は、長柱でありオイラーの式で座屈計算します。

ではこの条件式を満たしているかを検証するために、端末係数nを求めて計算していきましょう。今回の例題の支持方法が両端回転支持でしたので、端末係数n=1になります。よって、

90√n = 90、λ = 91.2

∴ λ > 90√n

よって、今回の柱は中間柱として取扱い、ランキンの式を用いて座屈計算をしていきます。

 

座屈計算をする

最後に座屈計算をしていきます。今回の例題では柱は中間柱ですので、ランキンの式を用いて座屈応力を計算します。ランキンの式の座屈応力の計算式は以下のようなものでした。

この計算式を用いて座屈応力を求めます。軟鋼のσ0(材料によって決まる応力)は333[MPa]、a(材料によって決まる実験的定数)は1/7,500になります。これらの値を代入して、座屈応力を計算していきましょう。

座屈応力σ = σ0 / (1 + a/n × λ²) = 333 / {1 + 1/(7,500×1) × 91.2²}

= 157.9[MPa]

 

答え

座屈応力：157.9[MPa]

 

まとめ

いかがだったでしょうか。もう一度今回の座屈計算の流れをおさらいしましょう。

まず初めに柱の断面二次半径と細長比を求めました。次に柱が中間柱か長柱かを選定するための条件式を検証しましたね。条件式に関しては柱の素材によって変わるものですので、どのような条件式になるかは覚えてしまいましょう。下の記事で解説をしています。

ランキンの式まとめ！座屈定数や長柱・中間柱の決定方法

中間柱か長柱かわかれば、ランキンの式を用いるかオイラーの式を用いるかがわかります。あとは公式通りに座屈計算をして終了でした。

今回の記事通りに計算をすれば、座屈計算は難しくありません。ぜひ復習を何度もして手順を完璧に覚えてしまってくださいね。

この記事は以上になります。最後まで読んでいただき、ありがとうございました。