梁の曲りづらさと梁の強さは、梁の断面形状によって決まります。今回は断面の強さを決める断面二次モーメントについての基礎を紹介していきましょう。

断面二次モーメントは高校物理では全く出てこないものなので、初めて勉強する人は難しく感じてしまうかもしれません。記事を読みながら、図は自分の手で書きながらイメージして勉強していってくださいね。それでは早速内容に入っていきましょう。

断面二次モーメントとは？曲げ剛性との関係は？

断面二次モーメントとは、材料の断面の性質の一つです。断面二次モーメントは完全に大学の物理の概念なので、ここでつまづく人が多いように見られますが、これの物理的意味を知ることで理解が深まっていきます。

ここでイメージをしてみましょう。材料の曲がりにくさについて考えてみます。

実体験からわかると思いますが、木材や鉄などはゴムよりも曲がりにくい材料です。同じように、紙は曲げようと思えば折りたたむことができますが、鉄板の場合は曲げるとパキッと2つに分裂してしまいます。

このように、同じ”曲げる”ということをしても、材料によって曲がったり曲がらなかったり、また材料によって折れたり2つに分裂したりします。この”曲がりにくさ”は材料によって決まるものです。

この”曲がりにくさ”を決めるための材料の指標として、材料の定数(ヤング定数)があります。

ヤング係数に関しては以前まとめた記事がありますので、それらを参照しましょう。

post

 

また、同じ材料でもその断面の形状によって曲がりにくさは異なってきます。

断面積の大きさは、材料の曲がりやすさに関係しています。紙一枚と紙100枚では、紙1枚の方が曲げやすいのは明確です。

同じ断面積でも、断面の形状によって曲がりにくさは違います。下敷きで考えてみましょう。平らな面は曲げやすいですが、下敷きを縦にして曲げることはできません。このように同じ断面積でも曲げにくさというものは大きく違います。

ここまでは材料の曲がりやすさには何が関係しているかを書いてきました。曲げモーメントに対して材料がどのくらい耐えることができるのかを判断するために断面二次モーメントは使われます。さて、断面二次モーメントがどのようなものなのかを軽く説明してきたところで、断面二次モーメントの導出方法を書いていきましょう。

 

断面二次モーメントの導出方法

断面二次モーメントの定義から最初に書きます。

x軸に関する定義は、

Ix = ∫y² dA

 

同様に、y軸に関する断面二次モーメントは、

Iy = ∫x² dA

になります。

 

image

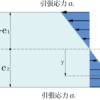
よって、上のような長方形のx軸に関する断面二次モーメントは、下の式のようになります。

Ix = ∫y² dA = [y³/3]0~b × a = ab³/3

曲げ応力度を計算するときなどには、部材図心軸に関する断面二次モーメントを計算する必要が出てきます。

図心に関するx軸の断面二次モーメントをIuとして考えてみると、

Iu = ∫y² dA = 2 × [y³/3]0~b/2 × a = ab³/12

となります。

図心に関するx軸の断面二次モーメントを求めているため、積分の範囲は0~b/2となります。

また、図心x軸に対して対象ですから半分の部材に関して断面二次モーメントを求めれば、その値を2倍したものが図心に関するx軸の断面二次モーメントIuです。

 

断面二次モーメント(軸から離れている場合)

次にもう少し一般的な図形の断面二次モーメントを考えていきます。

下の図を見てみましょう。

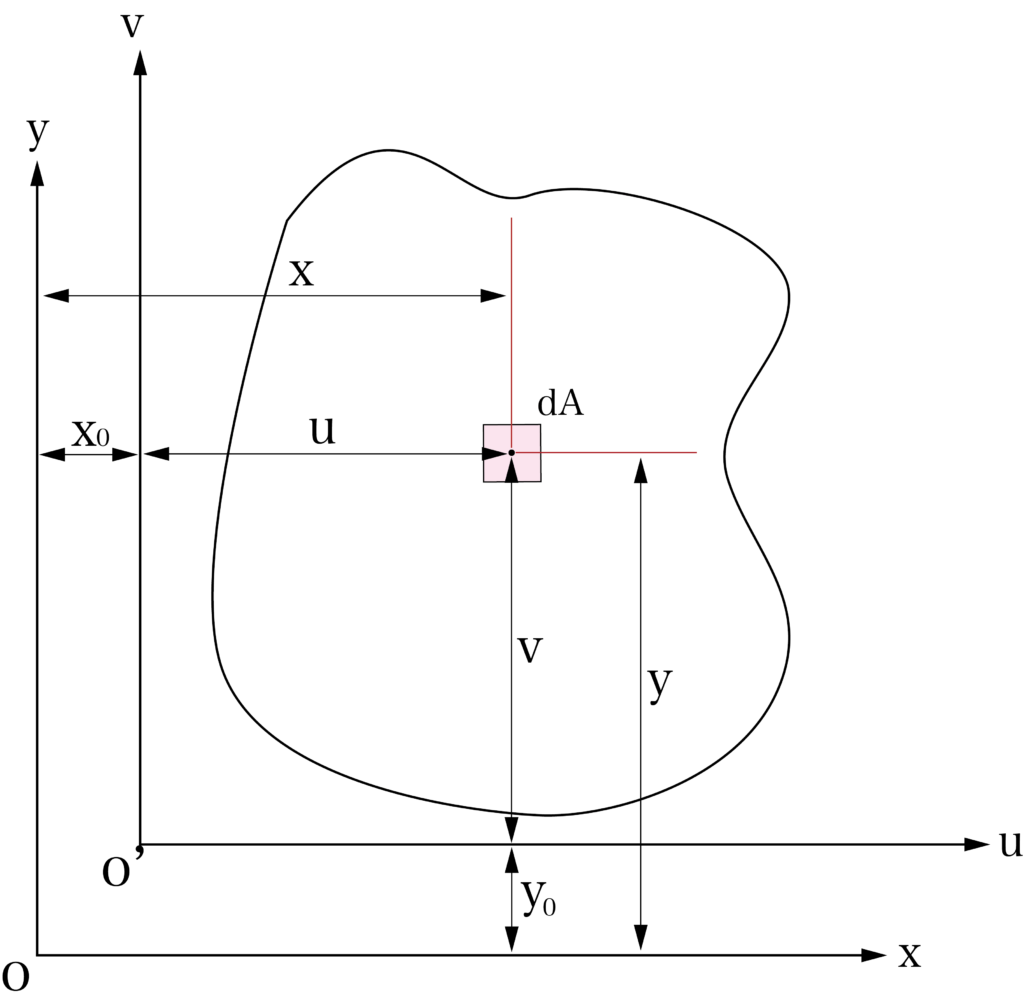
image

このような原点0とその座標軸x,yを考え、さらにその座標軸がu,vだけ並行移動した場合を考えていきます。

 

ある任意の物体についてのx軸に関する断面二次モーメントは、定義の式は以下のようなものでした。

Ix = ∫y² dA

元の座標軸と変化した座標軸の関係を考えると、

Ix = ∫y² dA = ∫(y0 + v)² dA = ∫y0²dA + 2∫y0vdA + ∫v²dA

= y0²A + 2y0Gu + Iu（∫vdA  = Guとして置き換え）

と変形をすることができます。

同様に、y軸に関する断面二次モーメントは、

Iy = x0²A + 2x0Gv + Iv

となります。

さらに、新しい座標軸の図心を原点(x0,yo)にもつ座標軸とした場合、上で示した式において

Gu = 0

Gv = 0

となりますから、

Ix = y0²A + Iu

Iy = x0²A + Iv

となります。

以上に示した式は、任意の座標(u,v)に関する断面二次モーメントを求める際によく用いられる式です。

この式も非常に重要となってくるので、導出過程を理解して、式は公式として暗記しておきましょう。

まとめ

今回の記事では断面二次モーメントについての基礎を紹介しました。断面二次モーメントがどういうものなのかをイメージしながら、それを数式として取り扱いましたね。

材料力学の中で特に重要となってくる概念の1つが今回の記事で紹介して断面二次モーメントです。この記事は何度も読みながら、断面二次モーメントの意味と導出過程、さらに公式までしっかりと理解するようにしてくださいね。

今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。