今回は梁の強さと、それに応じた変形について解説していきます。
梁のせん断力図と曲げモーメント図を書くと、梁にどれだけ変形させる力が働いているかを知ることができます。
今回の記事では、梁の変形について勉強していきましょう。
梁の変形については、梁の断面形状が大きく関係してきます。
実際にイメージしながら読んでいってくださいね。
梁の変形と曲げ応力
梁に荷重が作用すると、梁の内部にはせん断力と曲げモーメントが発生します。
それらは梁を曲げるように作用するものです。
せん断力図は梁の軸に垂直に発生するせん断力を表します。
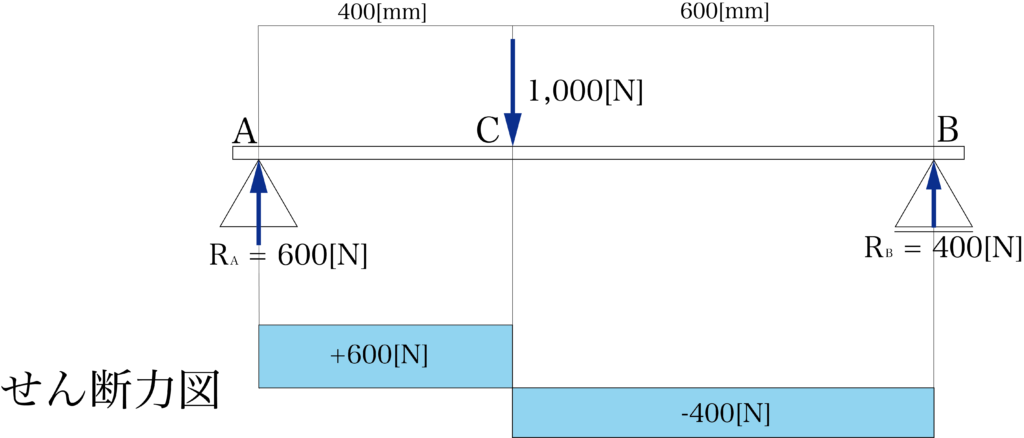
せん断力図とは上の図のようなものでした。
梁に働くせん断力を図式化したものです。
梁の長手方向に薄い層状の部分を考えると、梁の内側は圧縮、外側は引張を受けます。
材料にズレを与えて変形させるせん断力を発生します。
下の図を見てみましょう。
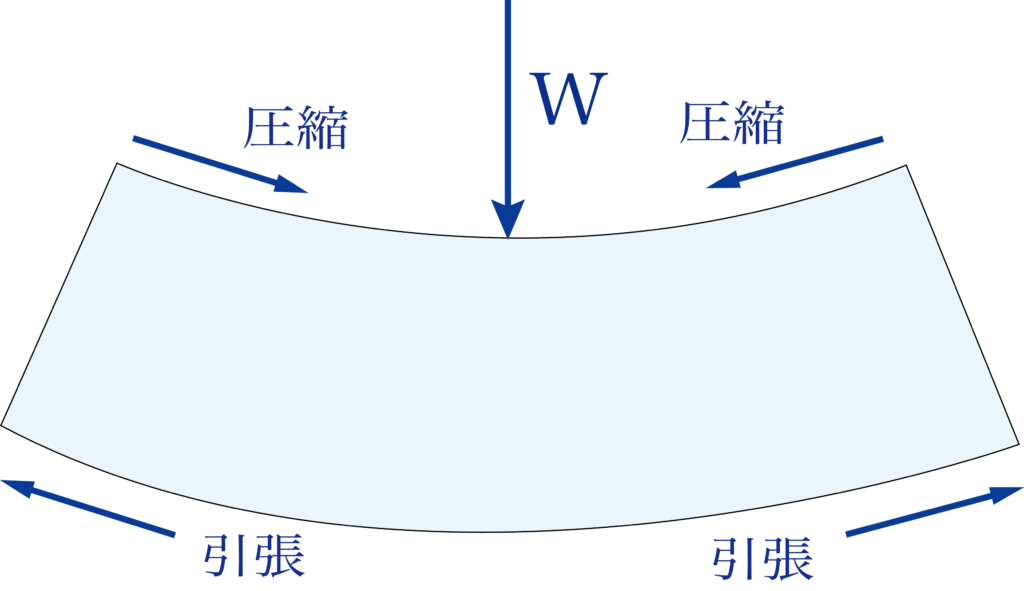
このように梁に荷重が働いた時、上の図のように材料は変形しようとしますが、梁の軸の上部分には圧縮力、梁の軸の下部分には引張力が働いていると考えることができます。
材料の内部では、せん断力による剪断応力と曲げモーメントによる曲げ応力が発生します。
応力とは、変形しないように材料内部に発生する抵抗力のことでした。
しかし、せん断応力は曲げ応力に比べてはるかに小さいため、材料力学においては一般的に梁の強さと曲げ応力の関係を考えて変形を取り扱います。
梁の断面形状
梁の断面形状も変形と大きく関係しています。
梁の荷重条件が限定されれば、断面積が大きいほど変形に対して強くなると考えられます。
それは応力の公式からも考えられることです。
一番右の応力 = 荷重(P)/断面積(A)を考えてみても、荷重が一定の場合は断面積が大きくなると応力が小さくなるので、材料内部に変形しないように発生する応力が小さくて済むというわけです。
逆に断面的が小さい場合は、応力が大きくなってしまうので、大きな応力に耐えられなくなった材料は変形してしまいます。
また、長方形断面の材料では、荷重に対して横長断面で使用するよりも、縦長断面で使用するようが強いことが経験から想像することができます。
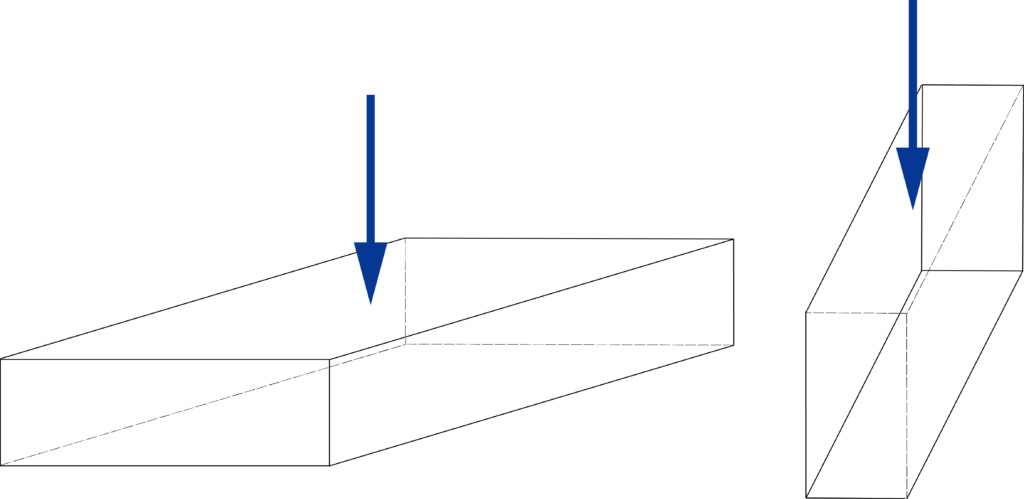
同じ断面積だったとしても、右の材料の方が変形しづらいことはイメージできますよね。
このように、梁の断面積と断面形状から、荷重を受ける梁に発生する曲げ応力が決定し、梁の強さを知ることができます。
逆に梁に許容できる曲げ応力を設定すれば、荷重条件からはりの断面寸法を決定することができます。
まとめると、同じ荷重条件なら断面積が大きい方が変形に対して強く、同じ荷重条件かつ同じ断面積の場合は、縦長断面の方が変形に強いということになります。
肩持ち梁のたわみとたわみ曲線
梁の材料内部では、引っ張りや圧縮の作用を受けますが、梁全体として緩やかに曲げられるように変形します。
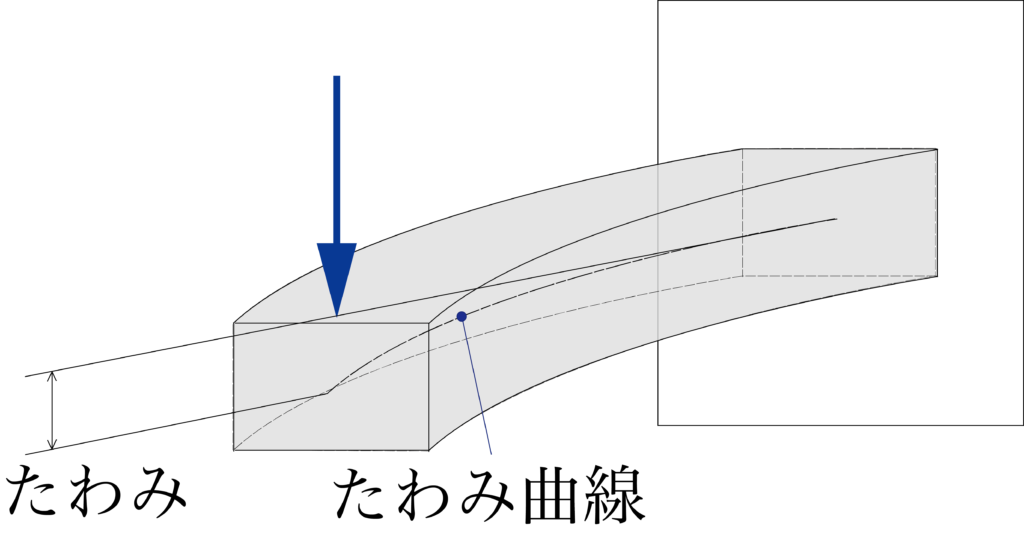
梁の変形や変形量をたわみと呼び、変形してできた軸の曲線をたわみ曲線と呼びます。
断面形状からたわみを予測したり、たわみから断面寸法を決定することができます。
たわみは荷重条件と梁の断面形状から求めることができます。
まとめ
今回は梁の変形についてまとめました。
梁の変形には断面形状が大きく関係しています。
同じ荷重条件でも、梁の断面形状によって変形量は異なってきます。
そのことを覚えておきましょう。
今回の記事は以上になります。
最後まで読んできただき、ありがとうございました。
