今回の記事では曲げモーメント図の書き方について勉強していきましょう。
曲げモーメント図とは、材料に働く曲げモーメントを図に表したものです。
英語ではB.M.D.(Bending Moment Diagram)と言います。
曲げモーメント図の書き方は、せん断力図の書き方を知っていると理解しやすくなります。
せん断力図とは、材料に働くせん断力を図式化したものです。
せん断力図に関しては、下の記事で詳しく解説していますので、まだ知らない場合は読んでおいてくださいね。
せん断力図の書き方について!両端支持梁に集中荷重が作用した時はどうなる?
では早速曲げモーメント図の書き方について紹介していきましょう。
目次
曲げモーメント図の書き方!集中荷重1つの場合
最初は両端支持梁に集中荷重が一つ作用していた時の曲げモーメント図に関してみていきます。
せん断力の求め方とせん断力図の書き方
せん断力図を書くときにもまず初めに支点反力から求めました。
せん断力図のときと同様に、最初に支点反力を計算していきましょう。
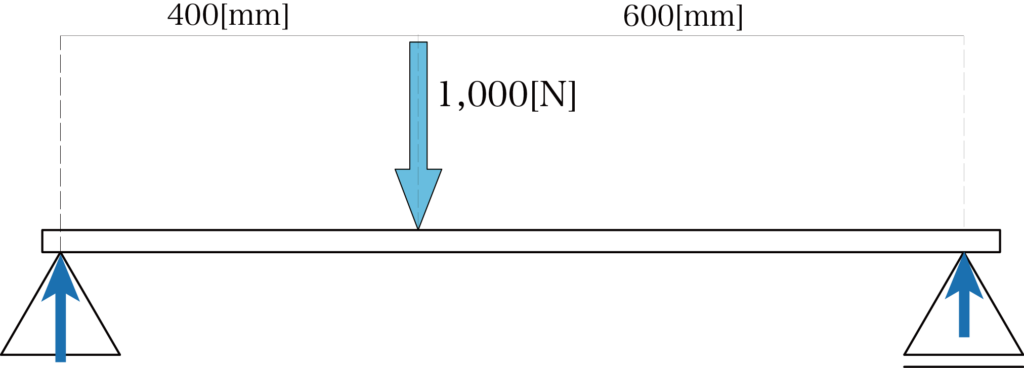
l1 = 400[mm]、l2 = 600[mm]として計算していきます。
RB = Wl1 / (l1 + l2)
= 1000×400 / (400+600)
= 400[N]
RA = W – RB
= 1000 – 400
= 600[N]
ここまでは高校物理の知識で解くことができますね。
これらの数値を図に書き入れると、以下のようになります。
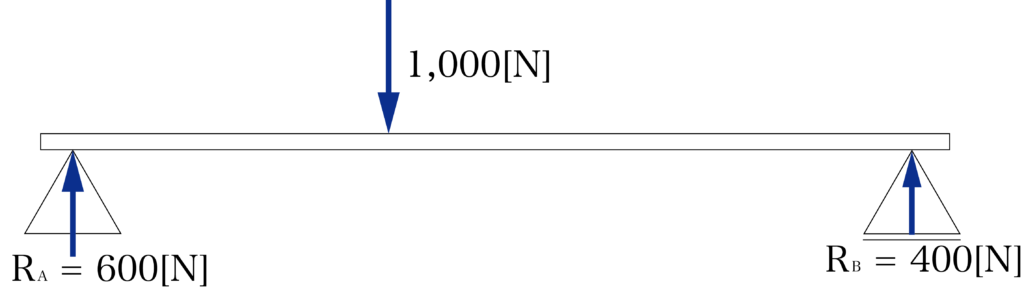
支点反力が求まったので、次にせん断力を求めていきます。
荷重点の左側のせん断力をF1、荷重点右側のせん断力をF2としましょう。

F1 = +600[N]になります。
次に荷重点右側のせん断力F2を調べます。

F2 = -400[N]と求めることができます。
荷重点左右のせん断力が求められましたので、これらをまとめてせん断力図にしましょう。
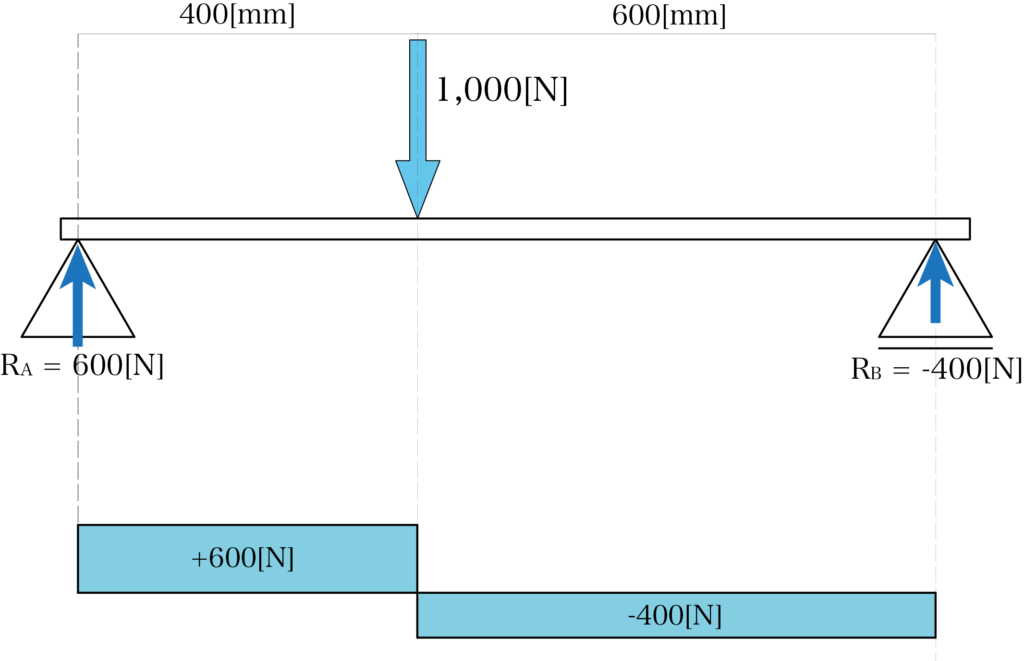
曲げモーメントの計算方法と、曲げモーメント図の書き方
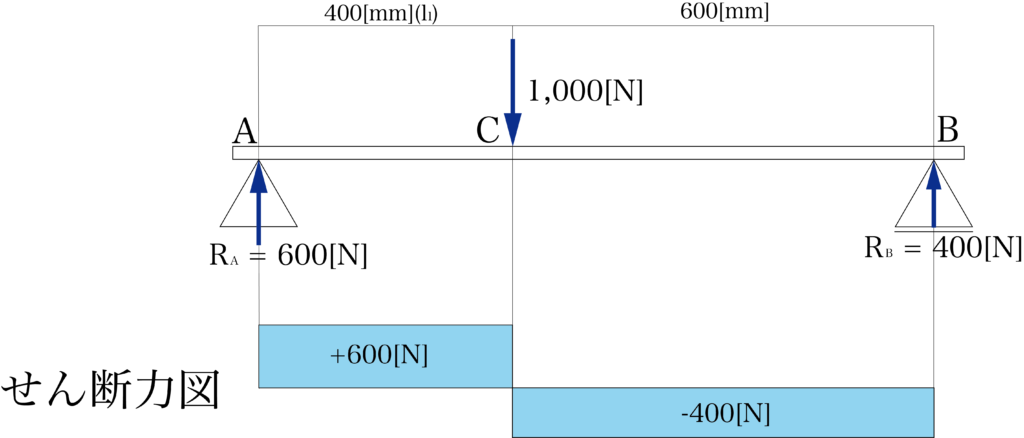
次に曲げモーメントの計算をしましょう。
左側の支点反力の作用点をA、荷重点をC、右側の支点反力の作用点をBをして計算していきます。
l1 = 400[mm]や、荷重の大きさなどは最後に代入します。
AC間の曲げモーメントは?(0≦x≦400)
x-x’の断面の荷重点Cの左側部材で、モーメントは下のようになります。
-RAx + MAC = 0
よって、MAC = RAx…(1)
x-x’の断面の右側部材では下のようになります。
-W(l1 – x) + RB(l – x) + MAC = 0
-Wl1 + Wx + RBl – RBx + MAC = 0
x(W – RB) – (Wl1 – RBl) + MAC = 0…(2)
梁の静止条件から力の総和とモーメントの総和はゼロです。
よって、W – RB = RA、Wl1 – RBl = 0…(3)
この式(3)を式(2)に代入します。
RAx + MAC = 0
よって、-MAC = RAx…(4)
式(1)と(4)から、MACの大きさは
MAC = RAx…(5)
RA = 600[N]ですので、これを代入すると、
MAC = 600x[N・mm]
これにより、AC間の曲げモーメントは比例定数が600の一次関数となります。
よってAC間の曲げモーメント図は以下のようになります。
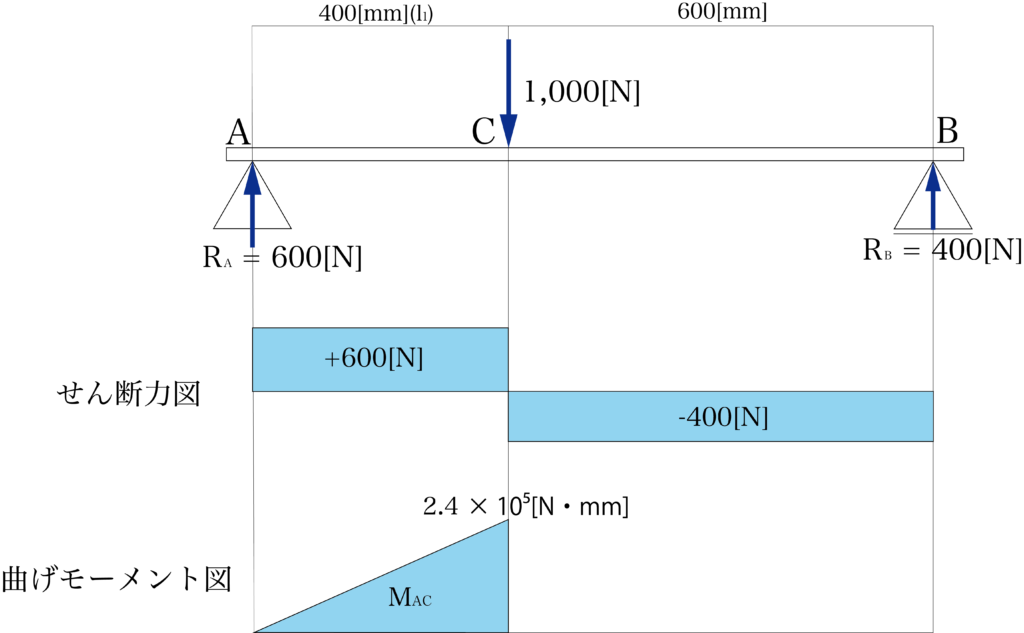
CB間の曲げモーメントは?(400≦x≦1000)
x-x'(仮想断面)の荷重点Cの右側部材で、モーメントは下の式のようになります。
+W(x – l1) – RAx + MCB = 0
+Wx – Wl1 – RAx + MCB = 0
x(W – RA) – Wl1 + MCB = 0…(6)
梁の静止条件から、
W – RA = RB、Wl1 = RBl…(7)
式(7)を式(6)に代入します。
RBx – RBl + MCB = 0
MCB = RB(l – x)…(8)
x-x’の右側部材で、
-MCB = RB(l – x)
式(8)と(9)からMCBの大きさは
MCB = RB(l – x)…(10)
l = 1,000[mm]、RB = 400[N]なので、これらを代入すると、
MAC = 400(1000 – x)
= 400000 – 400x[N・mm]
これを一次関数っぽく書き換えると、
MAC = -400x + 400000[N・mm]
CB間の曲げモーメント図は、傾き-400、切片4.0 × 10⁵の一次関数になります。
しかしxはA点が0なのを注意しましょう。
これを図に書き入れると下のようになります。
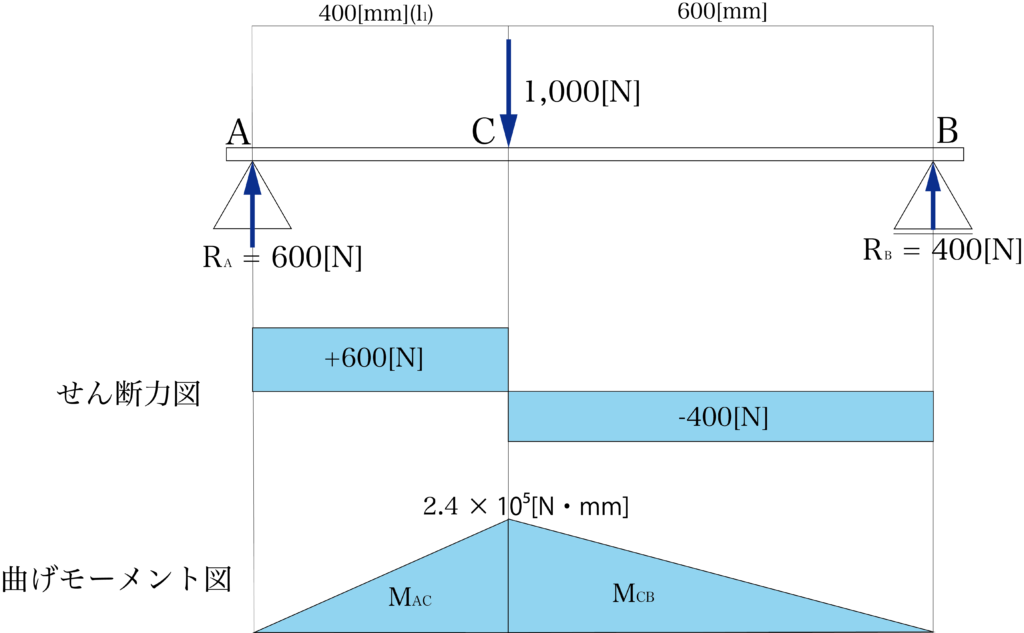
まとめ
今回は曲げモーメント図の書き方について紹介しました。
曲げモーメント図は大体、せん断力図と並べて書くのが普通です。
そのためせん断力図をしっかりマスターしておくことが重要になってきます。
また、曲げモーメント図のそれぞれのグラフの傾きは、せん断力の傾きと対応しています。
下の図を完成した図をもう一度おさらいしましょう。

AC間のせん断力は600[N]でしたが、同じ区間での曲げモーメントは、
MAC = 600x[N・mm]でした。
また、CB間のせん断力は-400[N]でしたが、同じ区間での曲げモーメントは、
MAC = -400x + 400000[N・mm]
このように、せん断力と曲げモーメントには微分積分の関係にあります。
これに関しては、違う記事で紹介します。
せん断力を微分すると、同じ区間の曲げモーメントの傾きになることを覚えておきましょう。
今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。