今回は両端支持梁に集中荷重が作用する場合の曲げモーメントについてまとめていきます。
梁に作用する外力は、梁に力のモーメントを与えます。
この記事では、反作用として梁の内部に生まれる曲げモーメントを求めていきます。
目次
集中荷重を受ける両端支持梁の曲げモーメントはどうなる?
では初めに1つの集中荷重を受ける両端支持梁の曲げモーメントについて求めていきましょう。
曲げモーメントとは、梁を曲げようと(変形させようと)するモーメントのことです。
上の図のような場合には、下の図のように材料を曲げようとするモーメントが働きます。
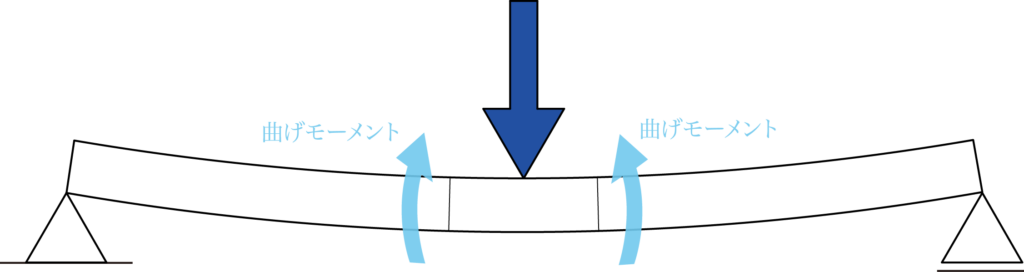
このように材料に荷重が作用すると、材料は固定されているので材料は変形させようとするモーメントが発生し、それが曲げ変形の場合はそれを曲げモーメントと呼びます。
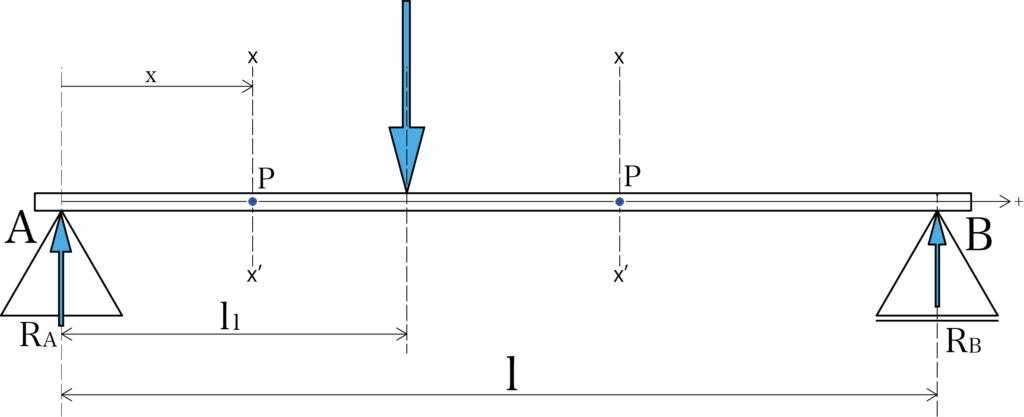
さて、もう一度最初の図を見てみましょう。

この図のような両端支持梁において、支点Aから距離xにある「仮想断面x-x’」を、視点Bに向けて移動させていきます。
荷重W、支点Aから荷重店までの距離l1、スパンをlとして、「断面x-x’」点Pを考え、点Pを中心とした力のモーメントの釣り合いを考えて大きさを求めていきます。
では次からは曲げモーメントの大きさを実際に求めていきましょう。
曲げモーメントの大きさの求め方は?
では曲げモーメントの大きさを求めていきましょう。

荷重点をCとして、AC間の曲げモーメントMACと、CB間の曲げモーメントMCBを求めます。
力のモーメントの符号は、反時計回りを+、時計回りを-として考えていきましょう。
また、荷重の大きさはWとします。
AC間の曲げモーメントは?(0≦x≦l1)
x-x’の断面の左側部材で、点Pを中心としたモーメントは下のようになります。
-RAx + MAC = 0
よって、MAC = RAx…(1)
x-x’の断面の右側部材では下のようになります。
-W(l1 – x) + RB(l – x) + MAC = 0
-Wl1 + Wx + RBl – RBx + MAC = 0
x(W – RB) – (Wl1 – RBl) + MAC = 0…(2)
梁の静止条件から力の総和とモーメントの総和はゼロです。
よって、W – RB = RA、Wl1 – RBl = 0…(3)
この式(3)を式(2)に代入します。
RAx + MAC = 0
よって、-MAC = RAx…(4)
式(1)と(4)から、MACの大きさは
MAC = RAx…(5)
CB間の曲げモーメントは?(l1≦x≦l)
x-x’の右側部材で、点Pを中心としたモーメントは下の式のようになります。
+W(x – l1) – RAx + MCB = 0
+Wx – Wl1 – RAx + MCB = 0
x(W – RA) – Wl1 + MCB = 0…(6)
梁の静止条件から、
W – RA = RB、Wl1 = RBl…(7)
式(7)を式(6)に代入します。
RBx – RBl + MCB = 0
MCB = RB(l – x)…(8)
x-x’の右側部材で、
-MCB = RB(l – x)
式(8)と(9)からMCBの大きさは
MCB = RB(l – x)…(10)
荷重点の左側も右側も、場所によって曲げモーメントの値が変わります。
そのため、曲げモーメントの値がxを含む式で表されます。
まとめ
今回は両端支持梁に1つの集中荷重が働く場合の曲げモーメントについてまとめました。
また、曲げモーメントの値の求め方についても紹介しました。
両端支持梁に1つの集中荷重に関しては、なかなか基本的なものですのでしっかり理解するようにしてくださいね。
今回の記事は以上になります。
最後まで読んでいただき、ありがとうございました。
