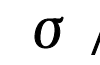建造物に使われている材料は弾性体です。
そのため、外力が加われば変形をします。
外力と変形量の関係を表す係数(ヤング率)を『応力ひずみ線図』からみていきましょう。
ヤング率は材料がどのくらい強いものなのかを図る尺度として考えることができます。
応力ひずみ線図に関しては、以前別の記事でも紹介しました。応力ひずみ線図についてまだあまり知識をもってない場合は、記事を読んでからこの記事を読むようにすると理解が深まると思います。
応力ひずみ線図について知識をもっている方は、それを考えながらヤング率について考えていきましょう。
ヤング率(縦弾性係数)とは?計算方法は?
それでは早速ヤング率についてみていきます。
固体の運動は、全体として並進運動、剛体としての回転および”ひずみ“に大別されます。
外力を取り除いたときに戻る限度のうちのひずみを扱うのが弾性体の力学です。
一般論ではバネの引っ張る外力とその伸びの関係などではなく、弾性体内部の各店で”ひずみ”と、それに伴って生じる”応力”の関係を考えていきましょう。
物体に変形を起させる力が加わっているときにには、その物体内にも力が生じます。これを応力といいました。
復元する力は作用力に等しいので、応力として外力を使うことができます。
金属などの固体に力を加えると、固体は変形します。
この応力によって生じた微小変形が”ひずみ“です。
これは固体の内部に応力が生じ、応力とひずみとが釣り合うために起こすもので、応力とひずみの間にはある関係が成り立ちます。
『応力ひずみ線図』で、弾性限度以下の範囲では。応力とひずみが比例をしました。
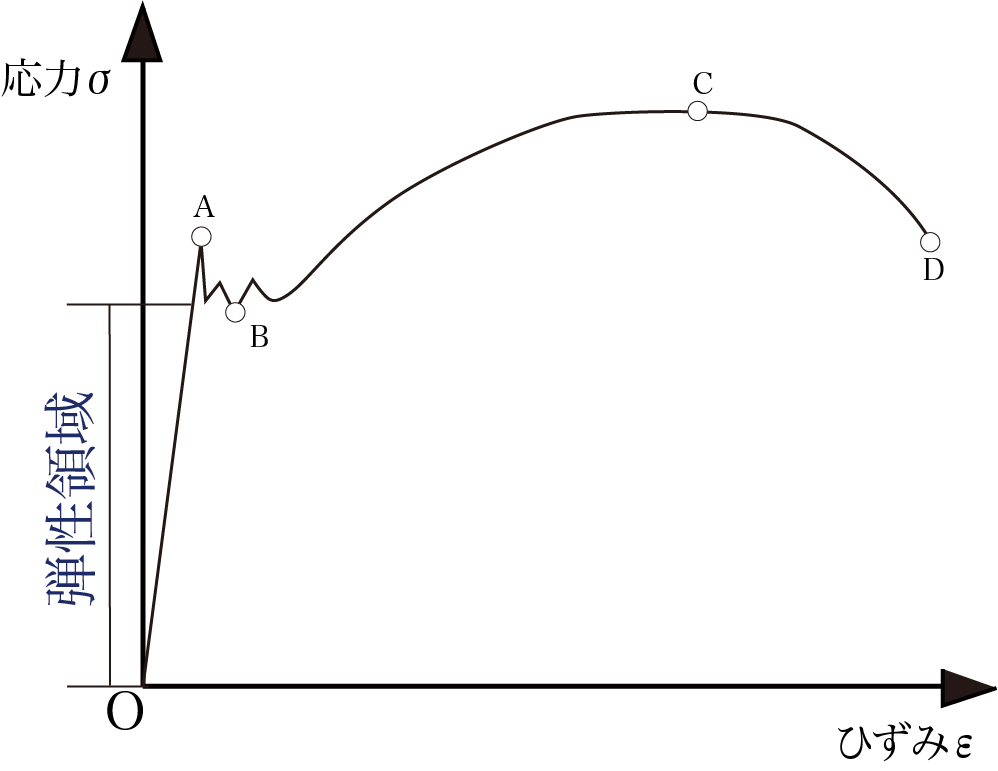
この範囲(弾性領域)の比例定数は、材料の変形に対する性質を表しています。
その性質を表しているのが、材料定数または弾性定数(ヤング率)です。
引張試験で得ることのできる『応力ひずみ線図』で、垂直応力σを縦ひずみεで割った弾性定数をヤング率または縦弾性定数Eと呼びます。
縦段数係数の単位は、応力を無次元のひずみで割るので、垂直応力[MPa]です。
しかしひずみが極端に小さいので値が大きくなるため、一般に[GPa]が使われます。
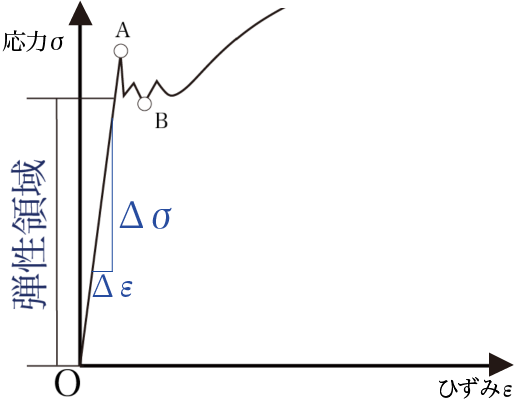
(E:ヤング率[GPaまたはMPa]、σ:垂直応力[MPa]、ε:縦ひずみ)
このヤング率Eは材料の強さの尺度となります。ヤング率(縦弾性係数)Eは色々な公式などでも登場しますから、この概念を覚えておくと公式に登場したときもスムーズに頭に入って行きます。
荷重と変形量の関係は?
ヤング率Eを求める垂直応力σは、材料の元の断面積Aと荷重Pで決まります。
ひずみのεは、材料の元の長さlと変形量のλで決まります。
これらの量を用いると、ヤング率は次のように表されます。
E = σ / ε
σ = P / A
ε = λ / l
これを代入すると
ヤング率E = σ / ε = (P/A) / (λ/l) = Pl / Aλ
このように式に式を代入することで荷重と変形量からヤング率を求めることができます。
まとめ
今回はヤング率についてしょうかいしました。
ヤング率とは応力とひずみの割合を表したものでしたが、そのヤング率によって材料のだいたいの強さをはかることができます。
イメージとしては材料の強さを測るものだと覚えておきましょう。
今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。