今回は縦ひずみとはちょっと違ったひずみである横ひずみに関して書いていきます。
縦ひずみ(ひずみ)に関して知りたい方は、以下のリンクから参照してください。
縦ひずみとは、おおざっぱにいうと材料に引張力(圧縮力)が作用したときに、材料がどれくらい伸びたか(縮んだか)の割合のことでしたね。
これは材料の軸方向をみたときの概念でした。
しかし実際に建造物に使われる材料は物体であり、3次元のものです。
そのため、材料の軸方向だけでなく違った方向にも伸縮しているはずです。
今回説明する横ひずみはその軸方向でない方向への伸縮を考えたものになります。
この記事の内容もとても重要ですので、しっかりと理解するようにしてくださいね。
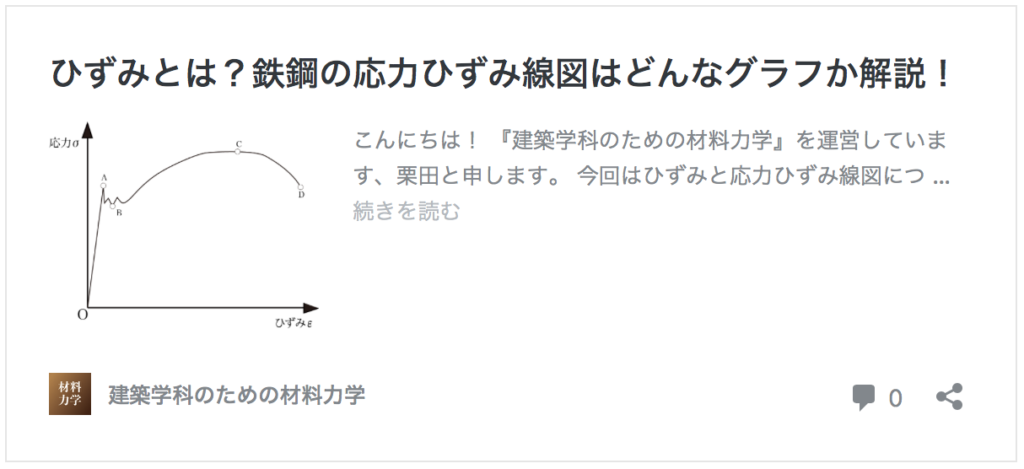
横ひずみとは?縦ひずみとの違いは?
では横ひずみに関して説明していきます。
材料は荷重の方向に沿った縦方向に変形をしますが、荷重の方向と垂直な横方向にも変形をします。
横方向の変形量σを材料の元も寸法dで割った値を、横ひずみε’としています。
横ひずみが『ε’』なのは、縦ひずみが『ε』で表されるからです。
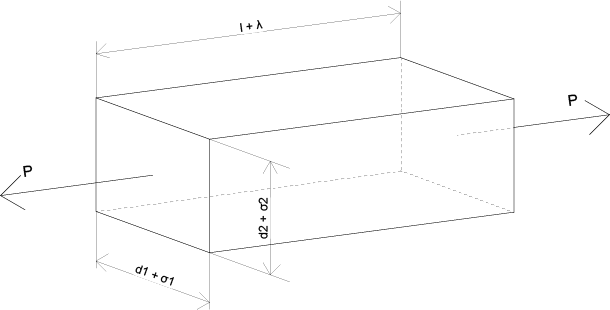
上の図は四角形断面の場合です。
断面の2辺方向の変化量σ1、σ2でひずみを考えています。
円形断面の場合も考え方は同様です。
直径をdとして、その直径の変化量をσとしています。
さて、ここまで横ひずみの説明をしたところで、横ひずみの公式を紹介しましょう。
ε’ = σ / d
(ε’:横ひずみ、σ:荷重の方と垂直な方向の変化量、d:材料の元の横の長さ)
この公式を理解したところで、もう一度上の図をおさらいしてみましょう。

荷重の方向と垂直な方向は2つありますね。
元の長さがd1の部分とd2の部分です。
この2つを考慮すると、今回の上の図の横ひずみは以下の式により与えられます。
ε1 = d1 / σ1
ε2 = d2 / σ2
このように四角形断面のような材料には荷重の方向と垂直な方向は2つありますから、同時に横ひずみも2つ導出することができます。
縦ひずみは材料にかかる荷重の方向のひずみのことでした。
横ひずみは、材料にかかる荷重とは違う方向のひずみのことというイメージで覚えておいてください。
横ひずみの符号はどうなる?
では次に横ひずみの符号(プラスマイナス)について触れておきましょう。
縦方向の変形量(λ)と横方向の変形量(σ)は、増加を正(+)・減少を負(-)としています。
材料の元の寸法は正なので、ひずみは変形量と同じ符号になります。
変形量とひずみの符号(増加が+、減少が-)
| 縦方向(λ、ε) | 横方向(σ、ε’) | |
| 引張荷重 | + | – |
| 圧縮荷重 | – | + |
ここではそれぞれの荷重に対して富豪がどのようになるかを説明するため、表を用いています。
しかし、ひずみは変形量と同じ符号になるので表を覚えていなくても問題ありません。
まとめ
今回は縦ひずみとは違った横ひずみに関してまとめました。
横ひずみとは、材料にかかった荷重の方向とは違った方向のひずみのことでしたね。
縦ひずみは材料のかかる荷重方向へのひずみ、横ひずみはそれ以外のひずみと覚えておくと整理しやすいかもしれません。
また、ひずみの符号は常に材料の変化量と一致しているということでした。
材料に引張荷重が働いている場合、荷重方向は伸びる(増加する)ので、それに応じて縦ひずみの符号は正になります。
「それぞれのひずみの符号は変化量と一緒」ということを覚えておきましょう。
今回の記事は以上になります。
最後まで読んでいただき、ありがとうございました。