今回はポアソン比の解説記事となります。
ポアソン比もまた、材料力学において重要な概念となりますのでしっかり理解するようにしましょう。
ポアソン比とは材料によって決まる材料定数です。
縦ひずみと横ひずみの比を表したものです。
縦ひずみと横ひずみに関しては以前の記事で詳しく解説していますので、これらを知りたい方は下の画像リンクから調べてみてください。
ひずみの概要について説明しておくと、ひずみとは荷重（引張・圧縮）がかかった材料がどれだけ変形しているかを表す指標になります。
荷重の作用線方向の材料の変形の割合を表したものが縦ひずみ、それ以外の方向への材料の変形の割合を示したものが横ひずみとなります。
この前提を頭に残した上で、今回の記事は読んでいってください。
ポアソン比とは？縦ひずみと横ひずみの割合？
では早速今回の記事の本題であるポアソン比について紹介していきましょう。
冒頭でも少し紹介しましたが、ポアソン比とは縦ひずみと横ひずみの割合です。
公式から紹介していきます。
ν = ε’ / ε
（ν：ポアソン比、ε’：横ひずみ、ε：縦ひずみ）
横ひずみ（ε’）を縦ひずみ（ε）で割った値がポアソン比（ν）です。
ポアソン比とは材料によって決まる材料手数であり、およそ1/3程度の数値をとります。
ここで材料に引張力がかかった場合を考えてみます。
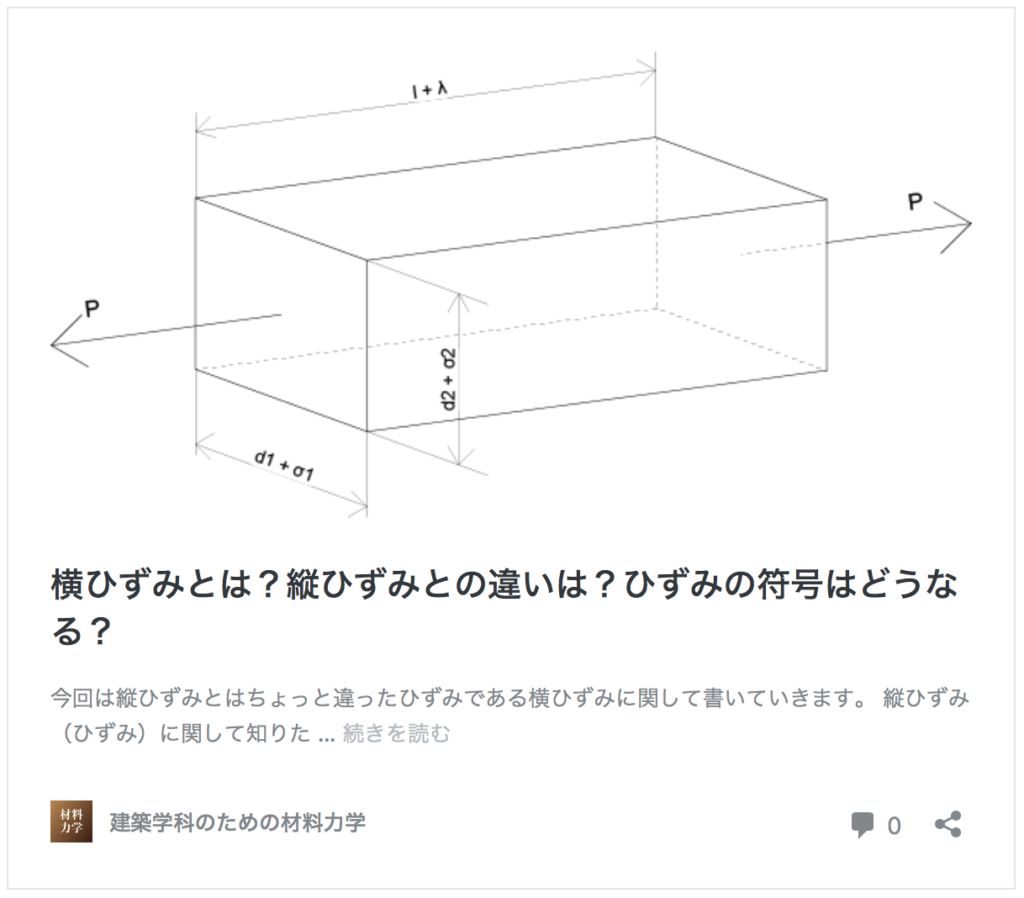
下の図をご覧ください。
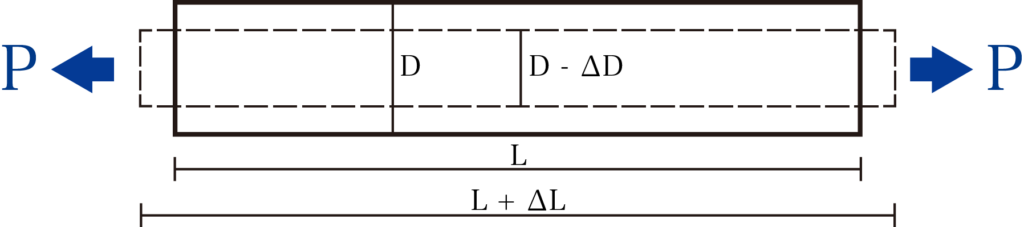
こちらは材料の両端に引張力がかかっている図です。
引張力は材料の側面（左右）に働いているので、当然材料は左右に伸びることになります。
それに対して材料の断面を考えてみると、D（断面の長さ）は縮むことになります。
この時のポアソン比を計算してみましょう。
ε = ΔL / L
ε’ = -ΔD / D（ΔDの符号はマイナスのため、ひずみ量をプラスにするために先頭にマイナスをかけている）
ν = ε’ / ε
= (-ΔD/D)/(ΔL/L)
こちらが上の図の場合のポアソン比となります。
ポアソン数とは？ポアソン比の逆数？
次にポアソン数について紹介します。
ポアソン数に関してはポアソン比を知っていれば簡単です。
m = 1 / ν
(m：ポアソン数、ν：ポアソン比)
ポアソン数（m）はポアソン比（ν）の逆数です。
これだけを覚えておけば問題ありません。
ポアソン比一覧
ポアソン比の一覧を紹介しましょう。
| 材料名 | ポアソン比 | 材料名 | ポアソン比 | 材料名 | ポアソン比 | 材料名 | ポアソン比 |
| 天然ゴム | 0.49 | タングステン | 0.28 | 銅 | 0.28~0.30 | ニオブ | 0.35 |
| 高密度ポリエチレン | 0.30 | アルミニウム | 0345 | 黄銅 | 0.35 | クロム | 0.21 |
| ポリエチレン | 0.35 | モリブデン | 0.31 | 鉛 | 0.44 | 砂岩 | 0.14~0.33 |
| ポリカーボネート | 0.39 | ガラス | 0.27 | 金 | 0.44 | 安山岩 | 0.07~0.22 |
| ポリアセタール | 0.32 | 銅 | 0.343 | スズ | 0.36 | 石灰岩 | 0.19~0.27 |
| エポキシ樹脂 | 0.37 | 鋳鉄 | 0.27 | タンタル | 0.35 | 大理石 | 0.25~0.38 |
参考：https://www.weblio.jp/wkpja/content/ポアソン比_主な物質のポアソン比
これらは問題では基本的に与えられるので、一つひとつ暗記しておく必要はありません。
まとめ
今回はポアソン比とポアソン数について紹介しました。
ポアソン比は材料によって決まっている、縦ひずみと横ひずみの割合です。
横ひずみを立てひずみで割った値がポアソン比となります。
そしてポアソン数とは、ポアソン比の逆数のことでした。
これらは今後の材料力学の学習をする際にとても重要になってくるので、しっかりとマスターしておいてくださいね。
今回の記事は以上になります。
最後まで読んでいただき、ありがとうございました。
