弾性係数とポアソン比の関係は？公式は？横弾性係数やせん断応力・せん断ひずみまとめ

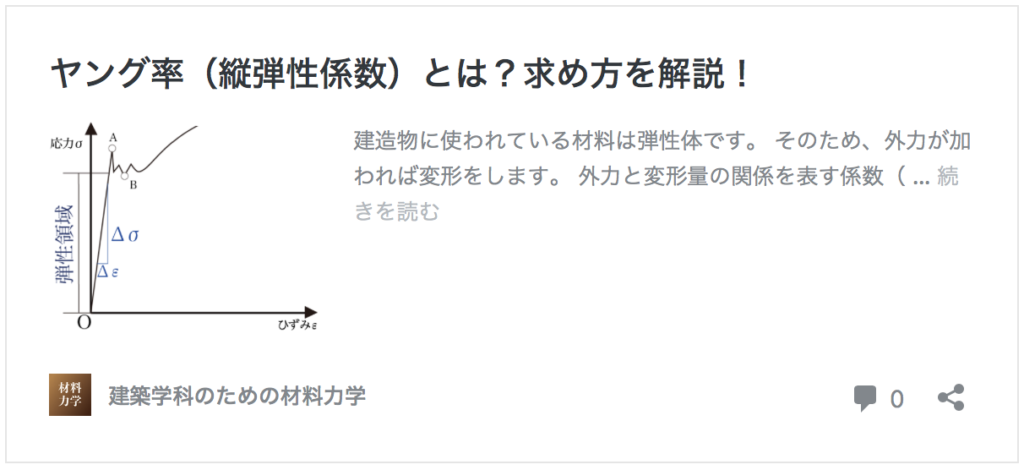
縦弾性係数（ヤング率）とは、材料のひずみと応力の関係を示したものでした。

 

ヤング率（縦弾性係数）の公式は以下の通りでした。

縦弾性係数に関しての詳細は以前の記事にまとめてありますので、そちらを参照ください。

 

さて、ヤング率（縦弾性係数）についてここまでは紹介しましたが、今回の記事では横弾性係数と弾性係数とポアソン比の関係について書いていきます。

弾性係数とポアソン比の関係は材料力学においてとても重要になってくるので、この記事は是非マスターしてくださいね。

 

 

せん断応力とせん断ひずみの求め方は？

では早速横弾性係数について紹介していきましょう。

 

せん断荷重を受ける弾性材料にも、軸荷重を受ける材料と同様に応力とひずみの比例関係が成り立ちます。

軸荷重を受けてひずみが発生した場合は、それと応力の関係を示したものが縦弾性係数でした。

今回紹介する横弾性係数は、軸荷重ではなくせん断荷重を受けて発生するひずみと応力の関係を示したものです。

 

下の図をご覧ください。

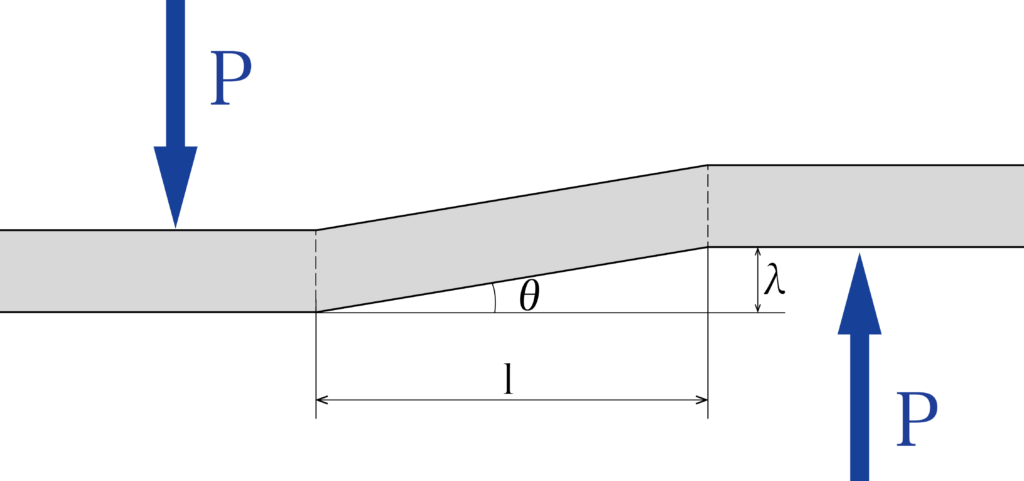
せん断力の求め方、せん断ひずみは以下で与えられます。

 

 

 

横弾性係数の公式を紹介！！

さて、上の公式たちを確認したところで、横弾性係数の公式を紹介します。

弾性係数は、縦弾性係数の場合も横弾性係数の場合も『応力 / ひずみ』の関係であることはかわりません。

 

上の公式群を横弾性係数の公式に代入すると、以下のような式になります。

G = τ / γ

= Pl / Aλ

また、θが微小のときは以下の関係が成り立ちます。

G = τ / γ

= τ / θ

 

これらの関係はとても重要ですので、マスターするようにしてくださいね。

 

 

弾性係数とポアソン比の関係は？公式を紹介！

最後に弾性係数とポアソン比の間に成り立つ関係について言及して終わりにしましょう。

縦弾性係数をE、横弾性係数をG、ポアソン比をνとして、これらの間には下の関係が成り立ちます。

この公式の導出過程を紹介しましょう。

 

最初に平面の応力を考えます、

ポアソン比をνとすると、主応力方向のひずみは

ε1 = (σ1 – νσ2) / E

ε2 = (σ2 – νσ1) / E

が与えられます。

これらの式から、主応力を主ひずみの日の関係は、

(σ2 – σ1) / (ε2 – ε1) = E / (1 + ν)

となります。

また、せん断応力とせん断ひずみの日の関係は 2τ/γ で与えられるので、モールの応力円（※別記事で解説）を想定すれば、上の式の左辺と同じになります。

(σ2 – σ1)/(ε2 – ε1) = E / (1 + ν) = 2τ / γ

これにせん断応力の式を変形したτ = Gγを代入すると、

E = 2G(1 + ν)の関係が導出されます。

 

弾性係数とポアソン比の関係に関しては難しい導出過程になりますので、覚える必要はありません。

公式だけは覚えておいてください。

 

 

まとめ

今回はせん断応力・せん断ひずみの求め方の解説から始まり、横弾性係数の公式を紹介しました。

さらに弾性係数とポアソン比の間に成り立つ関係も紹介しました。

 

今回の記事は非常に重要な内容が何個も出てきますので、繰り返し復習するようにしてください。

ブックーマークに入れて定期的に読み込むのも効果的ですよ。

 

今回の記事は以上になります。

最後まで読んでいただき、ありがとうございました。