ひずみとは？鉄鋼の応力ひずみ線図はどんなグラフか解説！

今回はひずみと応力ひずみ線図についてまとめていきます。

 

ひずみについては応力と同様今後の材料力学を学んでいく上でとても重要な概念となります。しっかりと理解して、今後も材料力学の学習もスムーズに進めていきましょう。

 

 

ひずみとは？材料がどれくらい歪んでいるかの割合？

さて、ではさっそくひずみについての説明をしていきます。ひずみは大学の物理で初めて登場する概念ですので、ゆっくり読んで理解を重視してください。

ひずみは材料に引っ張り力がかかった場合と圧縮力がかかった場合で計算方法が少し変わります。この2つを順々に説明していきます。

 

引っ張り力の場合のひずみ（引張ひずみ）の計算方法

まず初めにこの図をご覧ください。

 

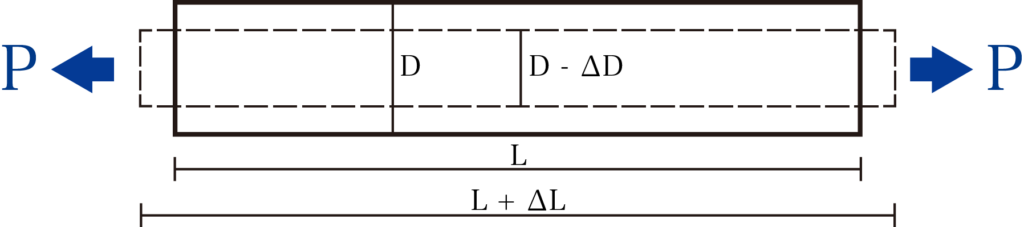
ある材料に引っ張り力Pを加えると、これに対応した応力のσが材料の内部に発生します。

応力は外力によって変形しないように仮想断面上に発生する内力のことでしたね。

 

材料には応力に比例した断面の収縮をする箇所と、伸びる箇所が存在します。

今回の場合は引っ張り力Pが働いているため、材料の側面部分は伸び、引っ張り力が働いている面は収縮しています。

材料側面の横の長さが最初はLだったのに対し、引っ張り力が働いていることによってΔLだけ伸びています。

ひずみとはこのどれだけ伸びたか（縮んだか）割合であり、ひずみ（ε）= ΔL/Lで求めることができます。

 

圧縮力の場合のひずみ（圧縮ひずみ）の計算方法

上の図は引っ張り力の場合のひずみの計算をしました。

次に材料に圧縮力が働いた場合のひずみの計算方法を説明していきましょう。

 

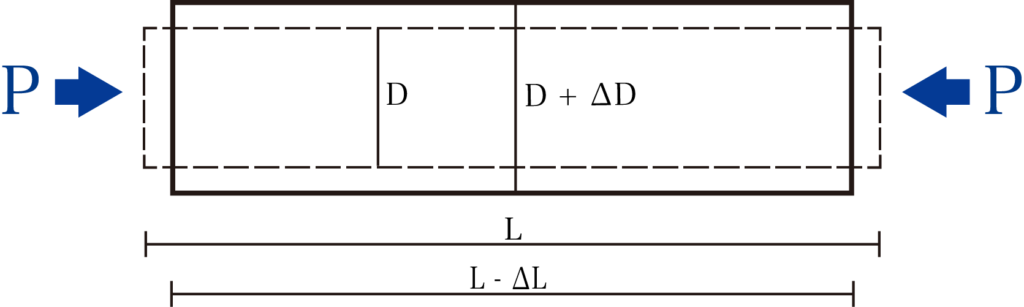
上の図を見てみましょう。

今回は材料を両端から押す圧縮力Pがかかっています。

すると材料は圧縮力のかかる面は広がり、材料側面の長さは圧縮力によって縮みます。

すると圧縮後の材料の長さはL-ΔLとなります。

 

ひずみの計算方法は引っ張り力と同じですが、ひずみは割合ですのでプラスの値にっていないといけません。

そのため、圧縮力の場合のひずみの計算式は、ε=-ΔL/L となります。

 

引っ張り力と圧縮力でΔLの符号の違いに混乱しそうですが、これは「ひずみは割合なので必ずプラスの値」と覚えておけば問題ありません。

「ひずみ」は漢字で書くと「歪み」であり、”ゆがみ”と同じ漢字です。

ひずみという言葉は日常生活ではあまり遭遇しませんが、「どれくらいゆがんでいるか」と置き換えて考えるとイメージしやすいかもしれません。

 

応力ひずみ線図とは？覚え方はある？

では次に応力とひずみの関係を表す応力ひずみ線図について紹介していきます。

 

これから紹介するのはは一般の構造物や機械部品に使われる鉄鋼材料の応力ひずみ線図です。

鉄鋼はほとんどの建物に用いられる材料ですので、この応力とひずみの関係を理解をしておくことはとても重要です。

早速グラフを見てみましょう。

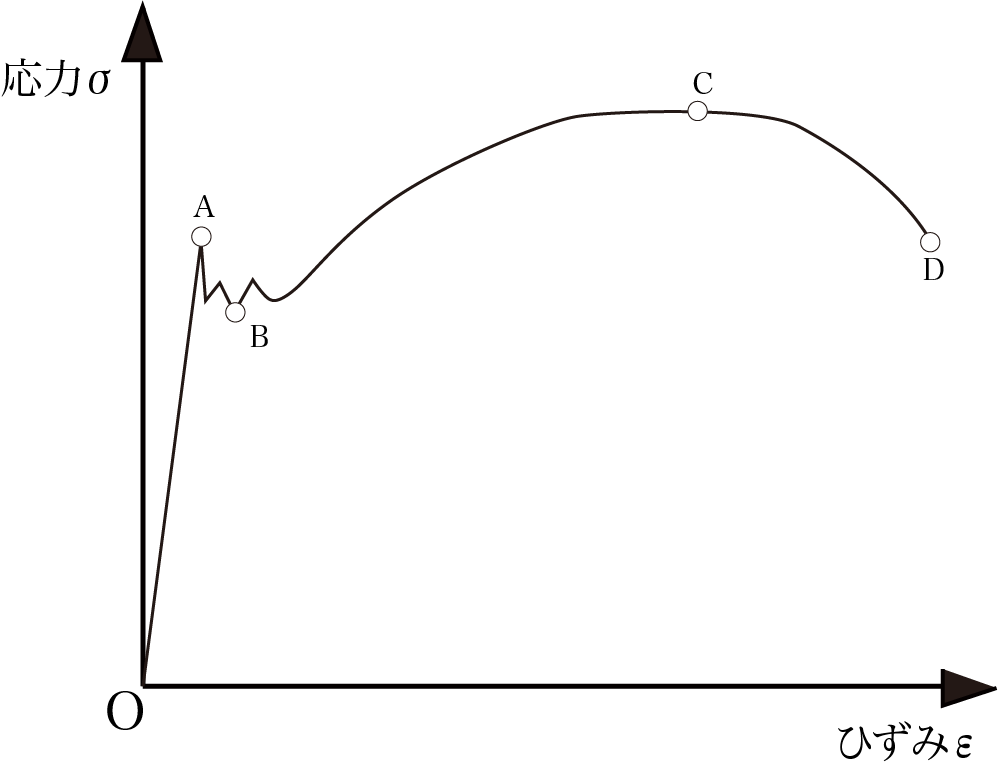
鉄鋼の応力ひずみ線図

 

 

ではアルファベットの振られたそれぞれの点の説明をしていきます。

A：上降伏点

A点からB点にかけてのギザギザした箇所を降伏領域と呼び、この領域では応力はほぼ変わらないのに対してひずみだけが増加します。その領域内でA点は応力の最大値となるところであり、上降伏点と呼びます。

B：下降伏点

A点が降伏領域の最大値だったのに対し、B点は応力の最小値になります。その最小値となる場所を下降伏点と呼びます。

C：引張強さ（極限強さ）

このC点は応力の最大値となる点です。引張強さといい、材料の強度を示す値です。

D：破断点

これは材料が破壊する点です。

 

他にも鉄鋼の応力ひずみ線図には特徴として説明できる点がありますが、今回は重要な箇所をピックアップしました。

最低限この図だけは覚えるようにしておきましょう。

 

 

まとめ

今回の記事では材料力学でこれまた超重要となる『ひずみ』に関してまとめました。

ひずみとは引っ張り力や圧縮力に対して材料がどれだけゆがんだのかという割合を示すものでした。

計算式は『ε=ΔL/L』でしたね。

 

また、建築物で最も頻繁に使われる材料の鉄鋼の応力とひずみの関係である『応力ひずみ線図』について説明しました。

鉄鋼の応力ひずみ線図は変なグラフであり、それぞれの点には特徴があることも勉強しました。

 

これらはどちらも構造計算をしていく上で重要な知識ですので、しっかりと理解しておきましょう。

今回の記事は以上になります。

最後まで読んでいただき、ありがとうございました。