断面係数とは？公式は？断面二次モーメントとの関係も紹介！

今回は断面係数について書いていきましょう。

『断面係数』という単語だけ見ても、断面に関する係数ということはわかります。

 

断面係数の説明をして行くには、断面二次モーメントに知識が欠かせません。

断面二次モーメントがどういうものなのかをまだ知らない場合は、以前断面二次モーメントについて書いた記事がありますので、それを参照してから勉強していきましょう。

それでは断面係数について解説していきましょう。

 

 

断面係数とは？意味について

最初に断面係数とはどんなものなのかを紹介していきましょう。

上でも少し書きましたが、断面係数は断面二次モーメントはセットで覚えると理解が非常に深まります。

 

断面係数は断面二次モーメントから求めることができます。

そのため、断面係数は断面二次モーメントとセットで覚えるとわかりやすくなります。

断面係数はその名の通り、断面に関する係数です。

材料の曲がりにくさに関して、断面二次モーメントの記事で紹介しましたが、同じ断面積の材料でも、断面の形状によって曲がりにくさは異なります。

 

断面係数の意味は断面に次モーメントと同じような意味であり、曲げモーメントに対してどれだけ抵抗できるかを意味します。

 

しかし、計算したいものによって断面係数と断面二次モーメントどちらを使うかは変えなければなりません。

断面係数は主に応力度を計算するときに、断面二次モーメントはたわみの計算をするときに使われます。

それでは実際に断面係数の公式を見ていきましょう。

断面係数の公式は？

では断面係数の公式について紹介していきます。

その前に、曲げモーメントと断面二次モーメントの関係についておさらいをしましょう。曲げモーメントは以下の式でも与えられました。

この公式を式(1)として、断面係数の説明をしていきます。

断面係数は、曲げモーメントMと曲げ応力σの関係を、梁の材質に関係せずに梁の断面形状から表すことのできる係数です。

下の図を見てください。

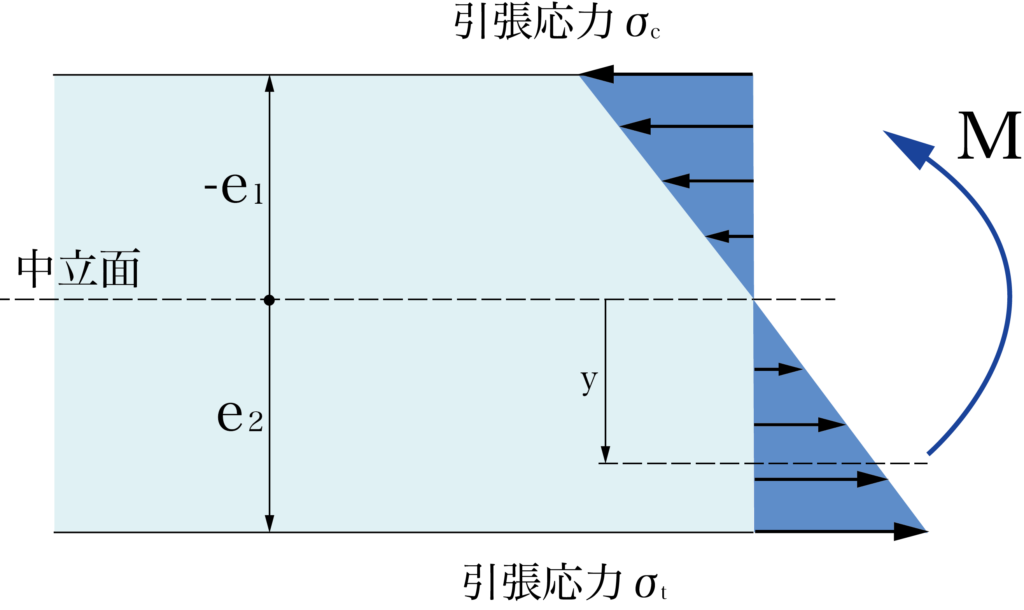
梁の変形と曲げ応力の関係から、

σ = E × y/ρ

1/ρ = σ/Ey…(2)

 

 

この式(2)を式(1)に代入してEを消去します。

M = EI/ρ = EIσ/Ey = σ × I/y

σ = M × y/I…(3)

ここで先ほどの図をもう一度確認しましょう。

式(3)のσ = M × y/Iを見てみると、曲げ応力σが、材質に関係なく曲げモーメントと断面形状で決まり、中立面からの距離yに比例し、梁の凹凸の両表面で最大になることを表しています。

距離yに、梁の凸面までの距離e1、凹面までの距離-e2を代入すると、

引張応力σt = M × e1/I

圧縮応力σc = -M × e2/I

となります。

ここで、I/e1=Z1、I/e2=Z2とすれば、

σt = M/Z1

σc = M/Z2

となるので、これを一般化すると以下の式になります。

σ = M/Z

 

これをZの式に変形すると、断面係数の公式が作れます。

 

断面係数はZで表されます。梁に発生する、上げ応力σが、断面係数Zに反比例するということがわかります。断面係数Zが大きくなると、一定の曲げモーメントMに対して、発生する曲げ応力σが小さくなるので、梁の強度が高くなることがわかります。

このように、断面係数は梁の強度を表す一つの指標だと思ってください。

まとめ

今回は断面係数についてまとめました。断面係数は、断面二次モーメントと同様に梁の強度を表すものと覚えてください。

断面係数と断面二次モーメントは、大学から登場する概念となり少し難しく感じられますが、記事を何度も読みながらしっかりマスターしてくださいね。これらをちゃんと理解していると、材料力学の今後の理解度がかなり進みます。

今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。