今回の記事では、断面係数の計算方法について紹介していきましょう。断面係数の計算は材料力学を学ぶ上で非常に重要になってきます。
梁の曲げ応力は曲げモーメントと断面係数から求めます。断面係数が大きければ、梁に発生する応力が小さくなり、梁は強くなります。
この記事ではその梁の強さを求めるために必要となる断面係数の求め方について解説していきます。
断面係数の計算方法
今回は実際に断面係数を求める例題を解きながら解説していきましょう。
下図の中空長方形断面(中が空洞の長方形断面)の断面係数を求めていきましょう。形状は長方形断面の中実材から中空部分を抜いたものと考えます。
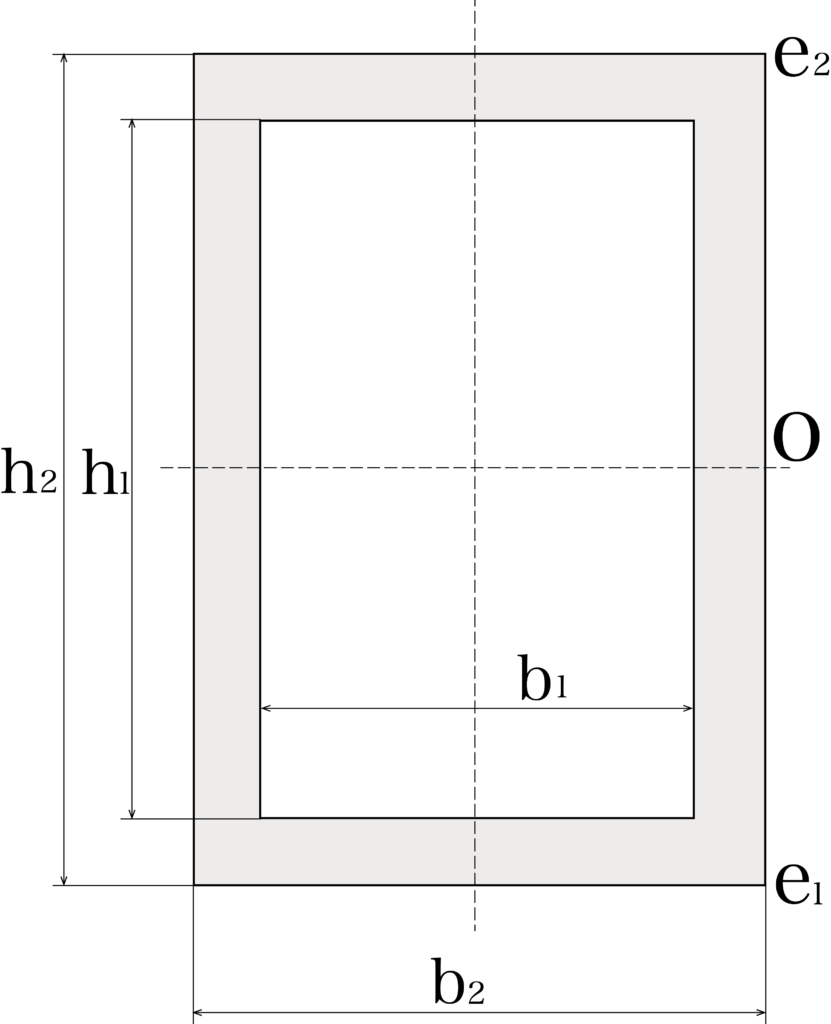
断面係数は、断面二次モーメントのように直接加減算できないため、はじめに断面に次モーメントIを求めてから断面係数Zを求めます。では早速断面二次モーメントを求めていきましょう。
断面二次モーメントを求める
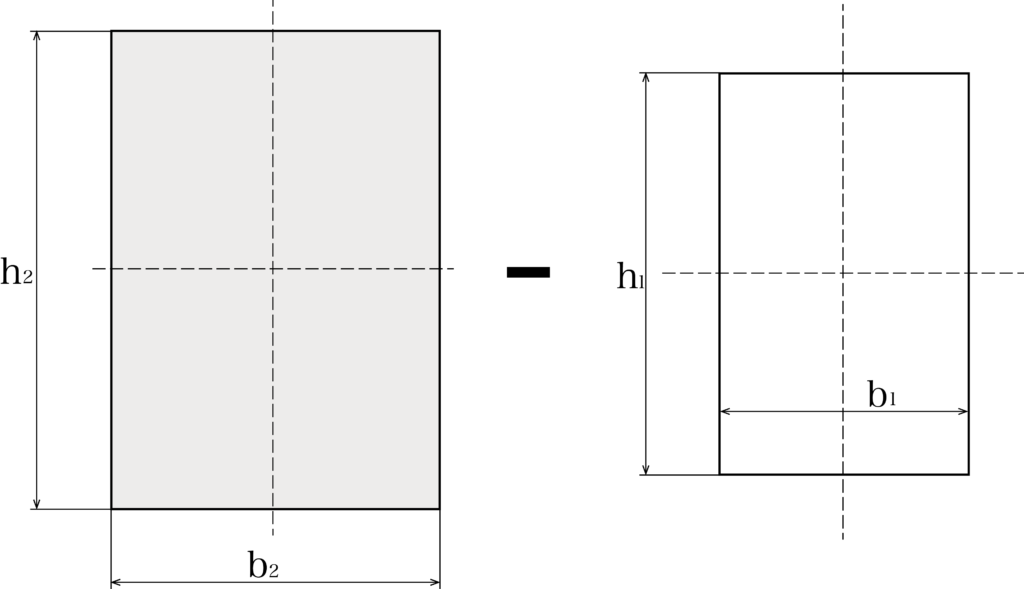
このように中空材を2つの部分に分けて考えていきます。左の図の断面二次モーメントをI1、右の図の断面二次モーメントをI2として、それを引き算して全体の断面二次モーメントIを出します。
I1 = b2h2³/12
I2 = b2h1³/12
よって、
I = I1 – I2 = (b2h2³ – b1h1³)/12
となります。
断面係数を計算する
次に中立面からの距離e1=e2から、断面係数を求めます。
e1 = e2 = h2/2
よって断面係数Zは、以下のように求められます。
I/e1 = I/e2 = Z
Z = I/e2 = 2/h2 × (b2h2³ – b1h1³)/12
= (b2h2³ – b1h1³)/6h2
このようにして最初に断面二次モーメントを求めた後に断面係数を求めていきます。中空材の断面係数の算出過程は以上です。
断面係数の公式と断面二次モーメントの関係
断面係数の求め方についてここまでは紹介してきました。断面係数と断面二次モーメントの関係について少し触れておきましょう。断面二次モーメントはIで表されましたが、断面係数の公式は以下のように表れます。
Z = I / e
(Z:断面係数、I:断面二次モーメント、e;図心から断面の端までの距離)
つまり、断面係数とは、断面二次モーメントを距離で割ったものです。
断面二次モーメントと断面係数は覚えると早い
今回は断面係数の計算の仕方を理解するために断面係数の算出過程について紹介しました。しかし実際に問題を解くときは、断面二次モーメントと断面係数については覚えてしまった方が圧倒的に早くなります。以前主な断面の断面二次モーメントと断面係数をまとめた記事がありますので、まだ覚えていない方は参考にしてください。
まとめ
今回は断面係数の求め方についてまとめました。断面係数は断面二次モーメントは足し算引き算できましたが、断面係数についてはそれができません。そのため、今回例に出したような中空材の断面係数は、まず全体の断面二次モーメントを計算してから断面係数を算出しました。断面係数の算出過程は多くの問題で必要とされますから、しっかりと理解しておいてくださいね。
また、断面二次モーメントと断面係数については算出を問われない問題に関しては覚えてしまっていた方がスピードが圧倒的に早くなります。たくさん問題をこなしていると覚えてくるはずなので、多くの問題を解いて慣れていってくださいね。
今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。