この記事ではたわみについて紹介していきます。この記事を読むと、たわみやたわみ角・たわみ曲線についての基礎を習得することができます。是非参考にしながら今後の勉強を進めていってくださいね。
梁は荷重を受けて変形をします。変形量は梁の断面係数や梁の強度の関係からは求めることができません。ここで、梁の変形量であるたわみを梁の強さから考えていきましょう。
目次
たわみ・たわみ角・たわみ曲線について
最初にたわみとたわみ角、たわみ曲線についてそれぞれを軽く説明しておきます。図を示しながら説明していきますので、頭でイメージしながら読んでいってくださいね。
たわみとは?
まず初めに、たわみとはどういうものなのかについてです。たわみ(曲げ)とは一言で表現すると、梁が荷重を受けて変形したときに、荷重を受ける前のy座標からどのくらいy座標が変化したかです。
この説明では分かりづらいので、下の図を見てみましょう。

たわみはこの図でいう、δ(デルタ)です。上の図の肩持ち梁は荷重Wを受けて図のように変形します。この時、材料は変形しているので、変形後の材料の材軸は図のように曲線になります。任意のC点は変形後にC’へと移動しますが、この移動したC’から変形前の材軸までの距離がたわみδとなります。たわみは材料のどの点で考えるかによって、その値が変わります。図からもわかる通り、肩持ち梁においてはたわみはA-A’間(自由端)で最大となり、B点に近づくにつれて小さくなっていきます。
たわみのイメージとしては、「変形前と変形後でどれくらい変形してるか」という覚え方をすると良いでしょう。
たわみ角とは?たわみとの関係は?
たわみについての説明が終わったところで、たわみ角について紹介していきましょう。たわみの概念の理解ができれば、たわみ角についてはそこまで難しいものではありません。
たわみ角についても図で説明していきます。下の図をご覧ください。
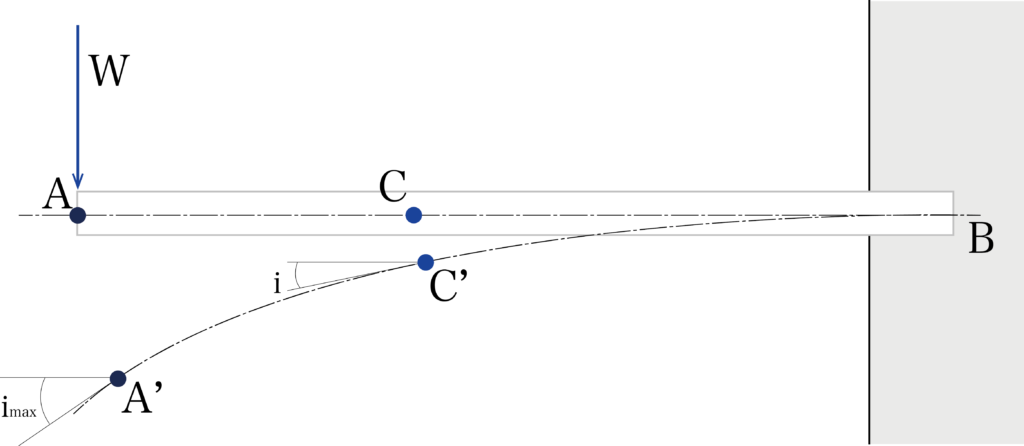
たわみ角はこの図のiの部分になります。たわみ角とは、変形前の材軸と変形後の材軸の接戦とのなす角のことです。
図からもわかる通り、たわみはA点で最大となると書きましたが、たわみ角についてもA点で最大となります。また、B点に近づくにつれてたわみ角も小さくなっていきます。たわみ角は通常i(あるいはθ)で示すので、それも覚えておいてくださいね。
たわみ曲線とは?
最後にたわみ曲線です。たわみ曲線についても図で説明しましょう。
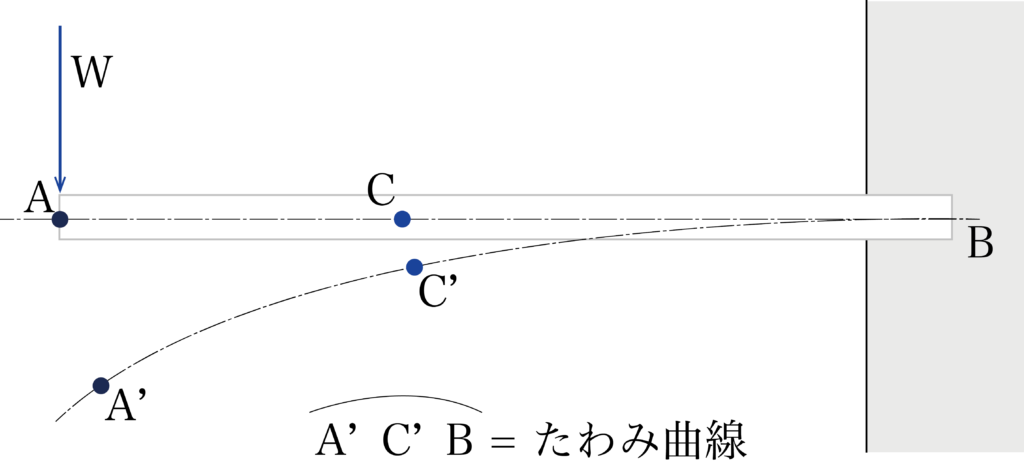
たわみ曲線とは、梁が変形した後の材軸(図のA’C’B)が作り出す曲線のことです。梁は変形すると曲線となるので、たわみ曲線と呼ばれます。図はわかりやすくするために曲線を大胆なものにしていますが、実際にはここまで変形するわけではなく、もっと緩やかな曲線になるということを一応頭に入れておいてくださいね。
たわみの計算方法・公式について
続いてたわみ・たわみ角・たわみ曲線について一通りの説明が終わったところで、最後にたわみの算出式・公式について紹介します。
梁のたわみ変形は、梁の種類や荷重条件によって大きく異なります。そこで、次の一般式で最大たわみと最大たわみ角を求める公式を紹介します。
最大たわみの公式
δmax = α × Wl³/EI
(δmax:最大たわみ、α:たわみ係数、W:荷重、l:梁の長さ、E:縦弾性係数・ヤング率、I:断面二次モーメント)
α(たわみ係数)とは梁の種類によって決まる値です。肩持ち梁に集中荷重が働く場合はα=1/3、両端支持梁に集中荷重が働く場合はα=1/16です。
また、分母にあるEIは、合わせて曲げ合成と呼ばれます。この二つはセットで使われることが非常に多いので、それも覚えておきましょう。
最大たわみ角の公式
imax = β × Wl²/EI
(imax:最大たわみ角、β:たわみ係数、W:荷重、l:梁の長さ、E:縦弾性係数・ヤング率、I:断面二次モーメント)
たわみ角の単位は[rad]です。こちらも分母はEIとなり、最大たわみ角は曲げ合成に反比例します。
また、上の公式からわかる通り、最大たわみも最大たわみ角などを求めるためには断面二次モーメントの計算が必要です。断面二次モーメントの求め方についてわからない場合は、下の記事を参考にしてくださいね。
まとめ
この記事ではたわみ・たわみ角・たわみ曲線について最初に説明してきました。たわみとは梁の変形量でした。たわみ角は任意の点の変形前の材軸と、変形後の材軸の接戦とのなす角のことでしたね。肩持ち梁においては、たわみとたわみ角はどちらも自由端で最大となります。
また、たわみ曲線について説明しましたが、たわみ曲線は変形後の材軸が作り出す曲線のことでしたね。たわみは材料力学などの構造力学の分野で非常に重要な概念ですので、何度も復習しながら理解を深めていってください。
この記事の最後で最大たわみと最大たわみ角を求める公式を紹介しました。これらの計算は、実際に練習問題や演習問題を解きながら使いながら慣れていくのが良いでしょう。
今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。