曲げ応力とは？計算方法や公式について紹介！

この記事では曲げ応力とはどんなものなのかを紹介していきます。

これを読むと曲げ応力とはどんな概念なのか、曲げ応力の基礎について習得をすることができます。

ぜひこの記事を参考にしながら、今後の材料力学の勉強に役立ててくださいね。

 

曲げおを受けた梁の凹側には圧縮応力が発生します。

対して凸側には引張応力が発生します。

この2つの応力を総称したものが曲げ応力です。

 

では早速内容に入っていきましょう。

 

 

曲げ応力とは？

最初に曲げ応力とはどんなものなのかを解説していきましょう。

記事の冒頭でも少し触れたように、曲げ応力とは梁に曲げモーメントが発生した時に梁に生じる垂直応力のことです。

文字だけではわかりにくいため、図を用いながら説明していきましょう。

 

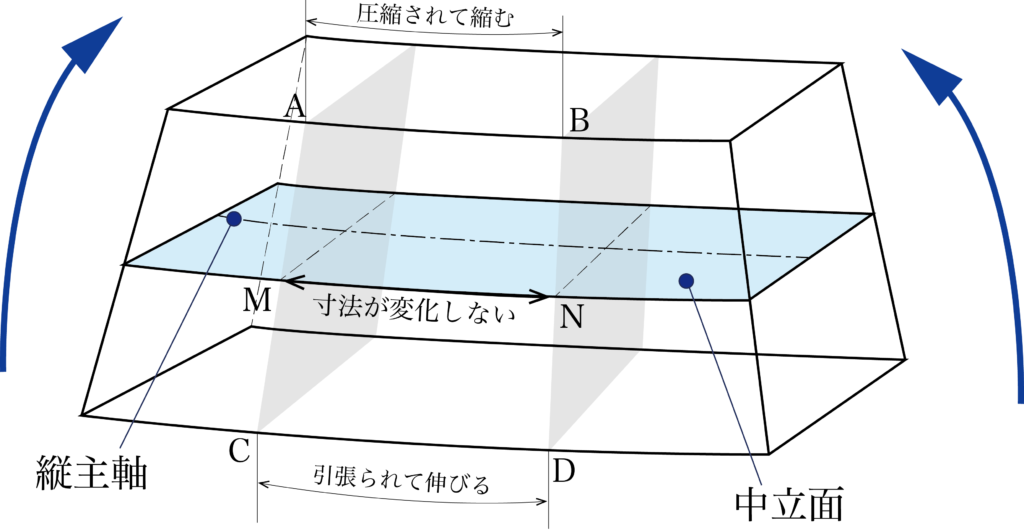
曲げられた梁の内側の距離ABは圧縮されて縮み、外側の距離CDは引っ張られて伸びます。

この内と外の両面から梁の内部に近づくにつれて、変形量は減少します。

そのため、縮みも伸びもない変形料がゼロの面MNが考えられます。

この面のことを中立面といいます。

 

梁の断面と中立面の交点を中立軸と呼び、任意の断面の重心をつないだ線を縦主軸と呼びます。

梁が変形すると、変形後の梁は円弧状になりますが、たわみ曲線については中立面で考えます。

 

 

上でも書きましたが、梁は円弧状に変形すると考えます。

中立面の長さは一定のため、中立面からの距離yの面PQでは、PQの長さからMNの長さを引いた寸法喧嘩が生まれます。

これを元の長さMNで割ったしきがひずみεとなります。

 

面のひずみεを求めてみましょう。

ひずみの公式はこちらでした。

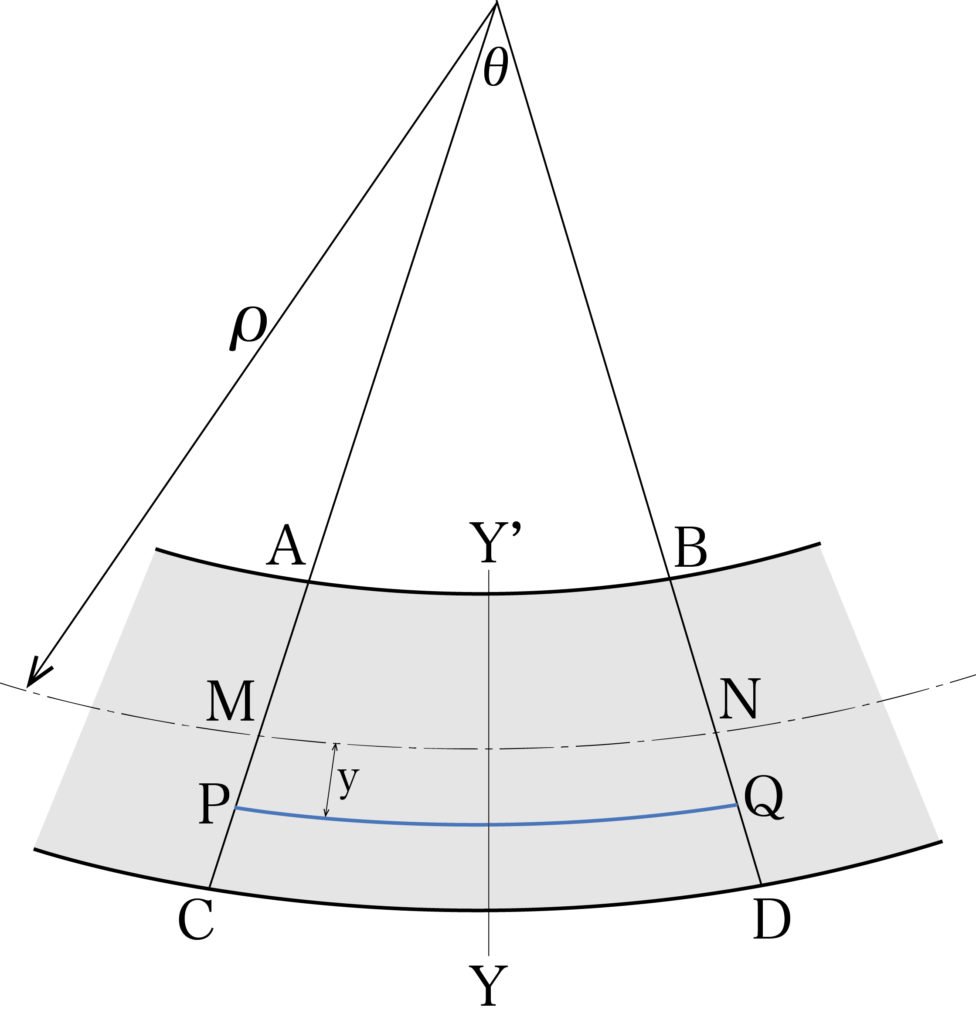
ひずみε = λ/l = (PQ-MN)/MN…(1)

 

MNとPQは、円弧の長さなので、中心角θ[rad]と半径の積で求めることができます。

MN = ρθ、PQ = (ρ+y)/θ…(2)

 

式(2)を式(1)へ代入して、ひずみを求めます。

ひずみε = {(ρ+y)θ – ρθ}/ρθ = yθ/ρθ = y/ρ…(3)

 

応力とひずみの定義は、以下のようなものでした。

よって、式(3)を上の定義に代入すると、

曲げ応力σ = Eε = Ey/ρ…(4)

この応力とひずみの定義から求めた式(4)が、中立面から距離yにある面に生じる曲げ応力です。

 

 

曲げ応力の最大値はどれ？

次に曲げ応力の大きさについて解説していきます。

上で計算した式(4)σ = Ey/ρについて考えてみましょう。

Eとρについては、一定の値となるため、中立面から任意の距離yにある面に発生する曲げ応力の大きさが、距離yに比例していることを示しています。

 

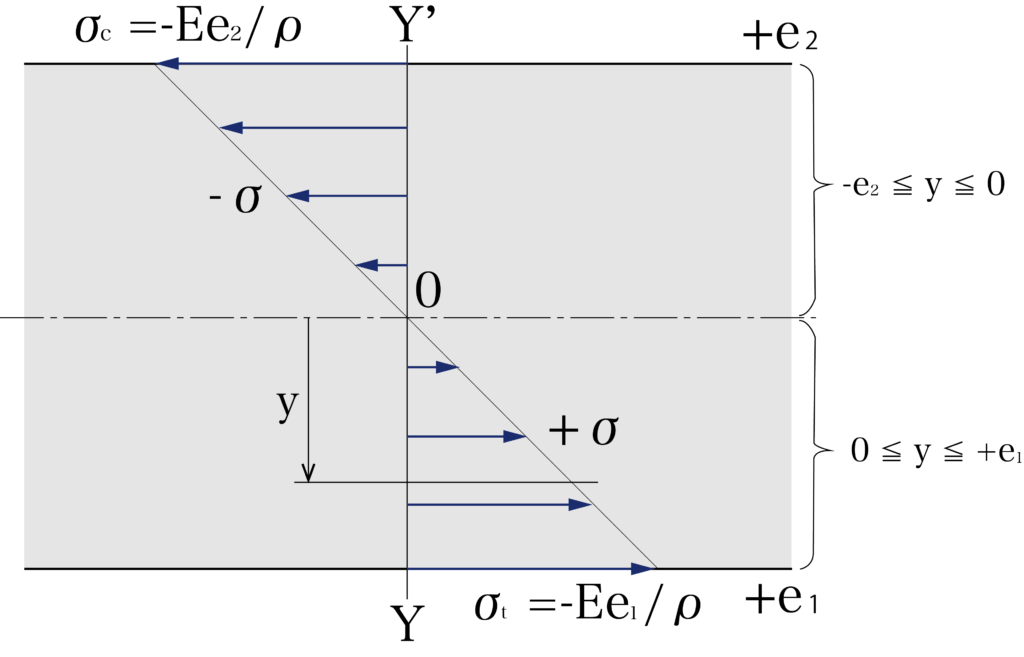
上のような仮想断面Y-Y’で、中立面を基準として、凸側のyの値を『+』、凹側の値を『-』、yを-e2≦y≦+e1とします。

yのあたいは材料の表面で最大となることは明確です。

それぞれの表面における曲げ応力を引っ張り側σt、圧縮側でσcとしましょう。

この値が図のように曲げ応力の最大値となります。

この応力は、縁で最大となることから縁応力とも呼ばれます。

 

曲げ応力は、材料の表面で最大値を取り、材料の中立面で最小値の0となることを覚えておきましょう。

 

 

まとめ

今回は曲げ応力について解説してきました。

曲げ応力とはどんなものなのか、また曲げ応力の計算方法について理解できたと思います。

曲げ応力の計算は非常に重要であり、よく問題でも問われるのでぜひマスターしておきましょう。

 

また、曲げ応力は、材料の表面(中立面から一番遠いところ)で最大値を取り、材料の中立面で最小値0

となることも紹介しました。

これを覚えていると、計算も理解も早くなるのでぜひ暗記しておいてくださいね。

 

今回の記事は以上になります。

最後まで読んでいただき、ありがとうございました。