ねじりモーメントの求め方・公式は？トルクとの関係は？

この記事ではねじりモーメントについて詳しく解説していきましょう。

ねじりを受ける棒材を軸と呼びます。

軸を回転させようとする外力はねじりモーメントを発生させます。

軸にずれ変形を与えます。

 

このねじりモーメントがどんな数式から導き出されるかを説明していきます。

 

 

ねじりモーメントとは？

最初に力のモーメントの復習からしていきましょう。

力のモーメントは高校の物理の力学の分野で登場する概念でした。

上の図のように、点Oから距離L離れた点AにOAと垂直に働く力Fがあったとします。

このとき、点Oを回転させることができる力のモーメントFLが発生するのでした。

 

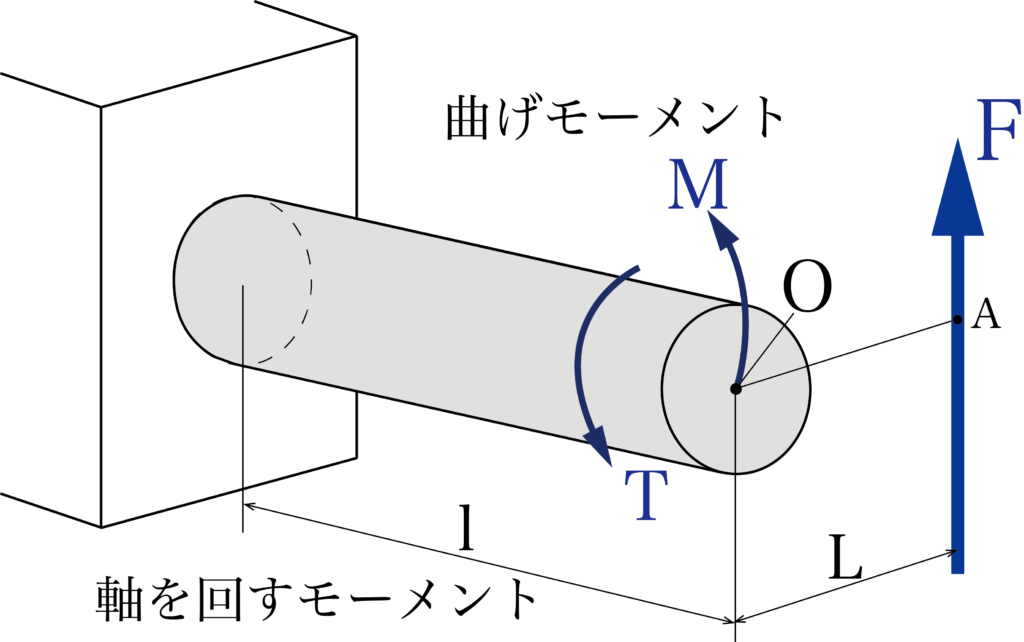
上の図のように長さlの軸の先端の中心Oから距離Lの点Aに、OAと垂直な力Fが働いていたとします。

上のような場合、軸を回そうとする力のモーメントTと、軸を曲げようとする曲げモーメントMが同時に発生します。

これはイメージしやすいのではないでしょうか。

 

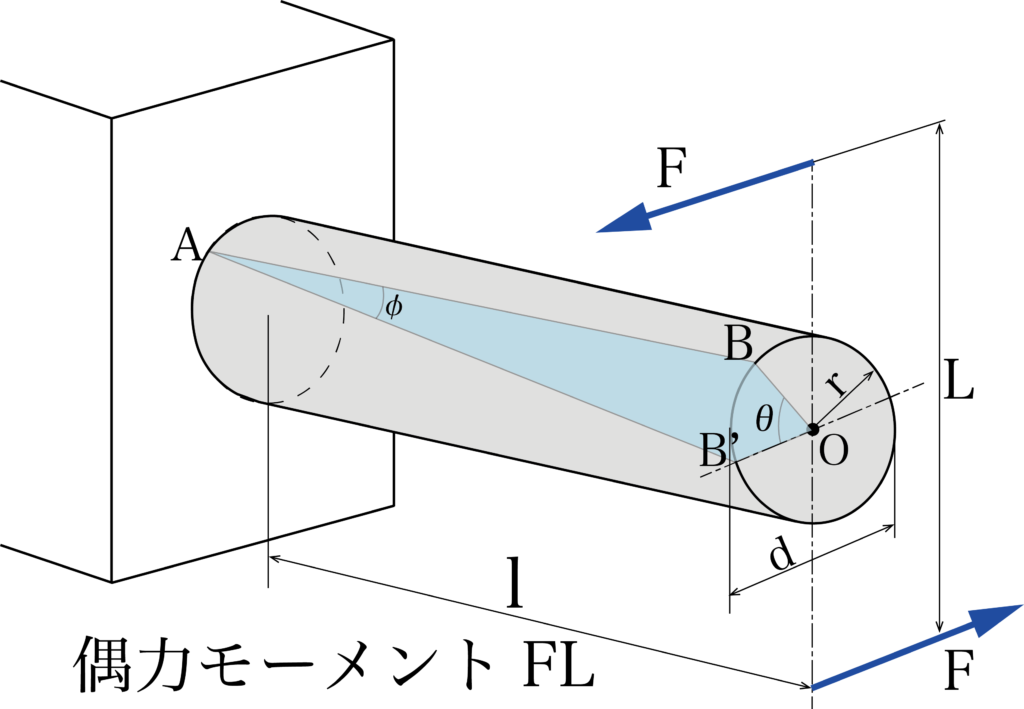
(φ:せん断角[rad], θ:ねじれ角[rad], d:直径[mm], r:半径[mm], r:半径[mm], l:長さ[mm], F:外力[N], L:腕の長さ)

図のような、示す力の大きさが等しく、並行で逆向きの一対の力Fを偶力と呼びます。

偶力Fが間隔Lで軸端に働くと、物体を回転だけを与える偶力モーメントFLが軸に作用します。

軸を回転させようとする力のモーメントをねじりモーメントTと呼びます。

機械工学の分野では、ねじりモーメントのことをトルクとも呼びます。

 

まとめると、ねじりモーメントの公式は以下のようになります。

 

 

まとめ

今回はねじりモーメントがどのようなものなのかについて説明しました。

ねじりモーメントはその名の通り、物体をねじろうとするものです。

ドアノブにもこのモーメントが利用されています。

 

今回の記事は以上になります。

最後まで読んでいただき、ありがとうございました。