この記事では円形柱の断面二次半径と、中実円形柱と中空円形柱の強さにつよさについて書いていきます。それぞれの断面二次半径を比較してどちらが柱として強いかを考えていきましょう。
荷重に対する梁の強さは断面係数、軸の強さが極断面係数で決まるように、柱の強さは断面二次半径で決まります。このことを踏まえた上で早速内容に入っていきましょう。
柱の強さは断面二次半径で決まる

上でも少し触れたように、柱の強さは断面二次半径によって決定されます。このことを覚えておくと、柱の座屈計算などで理解が深まると思います。
柱の座屈荷重・座屈応力を計算するときに、オイラーの式・ランキンの式を使いました。オイラーの式は柱が長柱のときに、ランキンの式は柱が中間柱のときに利用する式です。柱の強さが断面二次半径で決まることをわかりやすくするために、オイラーの式とランキンの式それぞれで座屈応力を計算する式を確認しましょう。
σ = n × π²E/λ²
(σ:座屈応力[MPa]、n:端末係数、E:縦弾性係数(ヤング率)[GPa]、λ:細長比(=l/k))
σ = σ0 / (1 + a/n × λ²)
(σ:座屈応力[N]、σ0:材料によって決まる応力[MPa]、a:材料によって決まる実験的定数、n、端末係数、λ:細長比(=l/k))
これらの式を見るとわかりますが、オイラーの式にもランキンの式にも座屈応力の計算式の分母に細長比λ(=l/k)が入っています。細長比λは柱の長さlを断面二次半径kで割ったものですが、断面二次半径が大きくなればなるほど、座屈応力が大きくなることがわかります。
中実・中空円の断面二次半径の比較
では中実円形柱と中空円形柱の強さについて考えていきましょう。
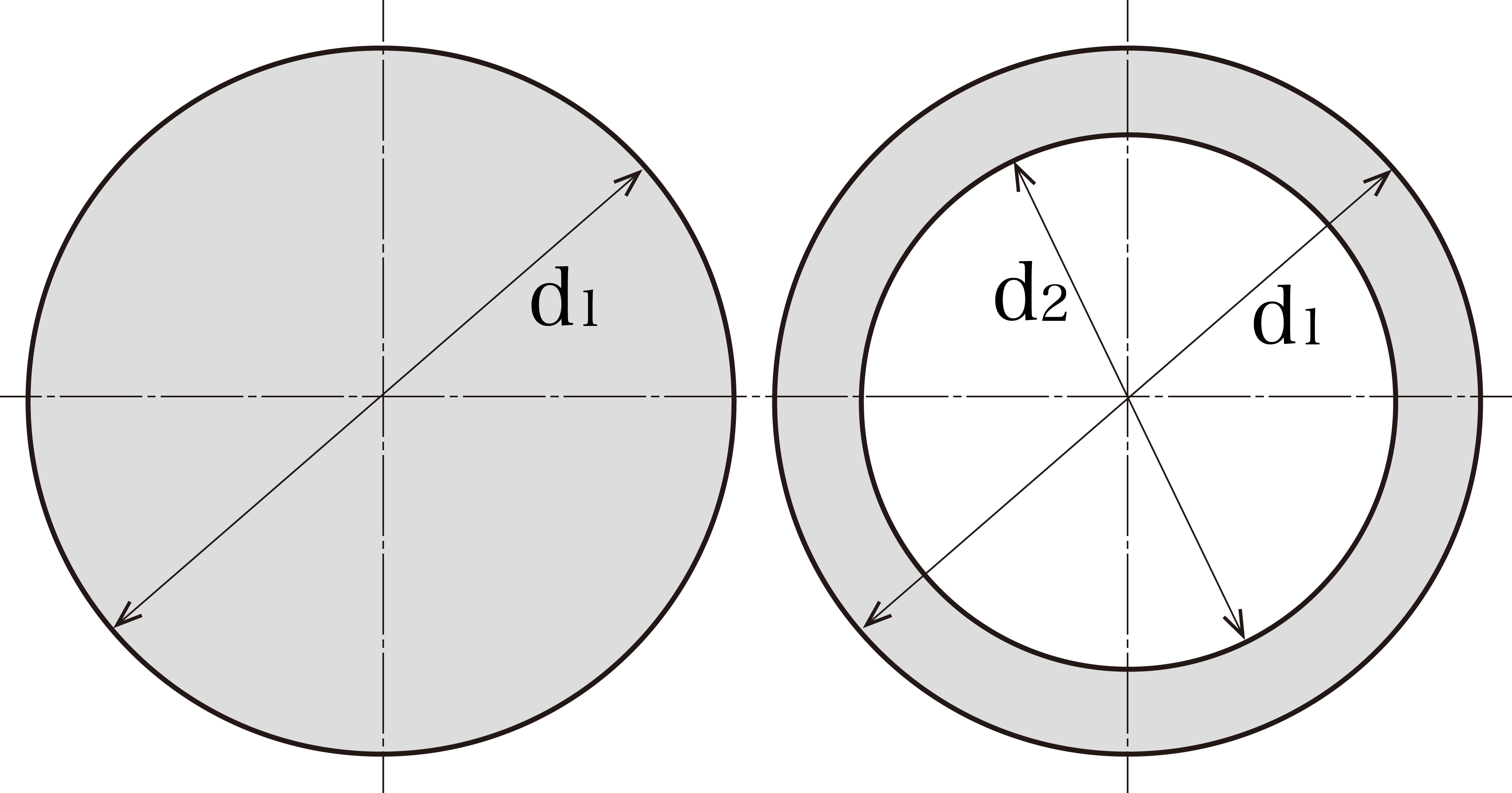
上の図のような外径の等しい中実円形と中空円形では、中空円形の方が大きな断面二次半径をもちます。この計算をしてみます。中実円形の断面二次モーメントをIs、断面二次半径をks、また中空円形の断面二次モーメントをIe、断面二次半径をkeとして計算していきましょう。
中実円形の断面二次モーメントIs = πd2⁴/64、
中実円形の断面二次半径ks = √(Is/As)
= √ (πd2⁴/64 × 4/πd2²) = √(d2²/16) = d2/4…(1)
中実円形の断面二次モーメントIe = π(d2⁴-d1⁴)/64、
中実円形の断面二次半径ke = √(Ie/Ae)
= √{π(d2⁴-d1⁴)/64 × 4/π(d2²-d1²)} = √{(d2²+d1²)(d2²-d1²)/16(d2²-d1²)} = √(d2²+d1²)/4…(2)
中実円形の断面二次半径をksはd2/4なのに対し、中空円形の断面二次半径をkeは√(d2²+d1²)/4となります。よってks<keとなり、外径が同じの場合は断面二次半径は中空円形の方が大きくなります。
これより、上では断面二次半径が大きくなればなるほど座屈応力が大きくなると書きましたが、中実円より中空円の方が断面二次半径が大きいので、座屈応力は中空円形の方が大きくなります。これは不思議に思うかもしれません。
中実円より中空円の方が荷重をかけられるわけではない
さて、上で断面二次半径を計算してきましたが、外径が同じの場合は中実円より中空円の方が断面二次半径が大きくなるのでしたね。
しかし、「中空円形柱の方が大きな荷重をかけても大丈夫なのか?」というと、そうとは限りません。それは、座屈荷重を計算するときに断面積をかけるからです。
オイラーの座屈応力を求める計算式は、σ = n × π²E/λ²でしたが、応力に断面積をかけると荷重が求められるのでした。これより、
座屈荷重P = σ × A = n×π²E/λ² × A
となり、断面積は中実円の方が中空円より大きいので、座屈荷重が大きくなることがあります。このことの詳しい詳細に関しては、中実円と中空円の座屈応力と座屈荷重の例題で見ていきましょう。
まとめ
今回の記事では、中実円と中空円の断面二次半径について見てきました。柱の強さは断面二次半径で決まります。
また、外径が同じの中実円と中空円の断面二次半径を実際に計算しましたが、不思議なことに中空円の方が断面二次半径が大きくなるのでしたね。しかし断面二次半径が大きい中空円の方が大きな荷重をかけることができるかというと、そういうわけでした。コチラの演習問題でその詳しい詳細を書いていますので、そちらを参照してください。
今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。