力の作図方法(力の合成と力の分解について)

この記事では力の作図方法について紹介していきます。

高校の力学でも勉強した方が多いと思いますが、力はベクトルで表すことができます。高校物理を思い出しながらこの記事を読むと、さらに理解が深まっていくでしょう。

力をベクトルで表す方法についてすでに理解している方は、この記事を飛ばしてもらって構いません。しかし力の作図方法は、別記事で紹介している力の作図による「クレモナ図法」などの解法の基礎となるものなので、しっかり理解する意味でもこの記事を読んで復習するのも良いでしょう。

それでは早速内容にはいっていきます。

 

力の作図法：力の合成と分解

作図法による力の合成

まずはじめに力の合成ついてです。

記事冒頭で力はベクトルによって表すことができると書きましたが、力はベクトルのように足し算や引き算をすることができます。下の図を見てみましょう。

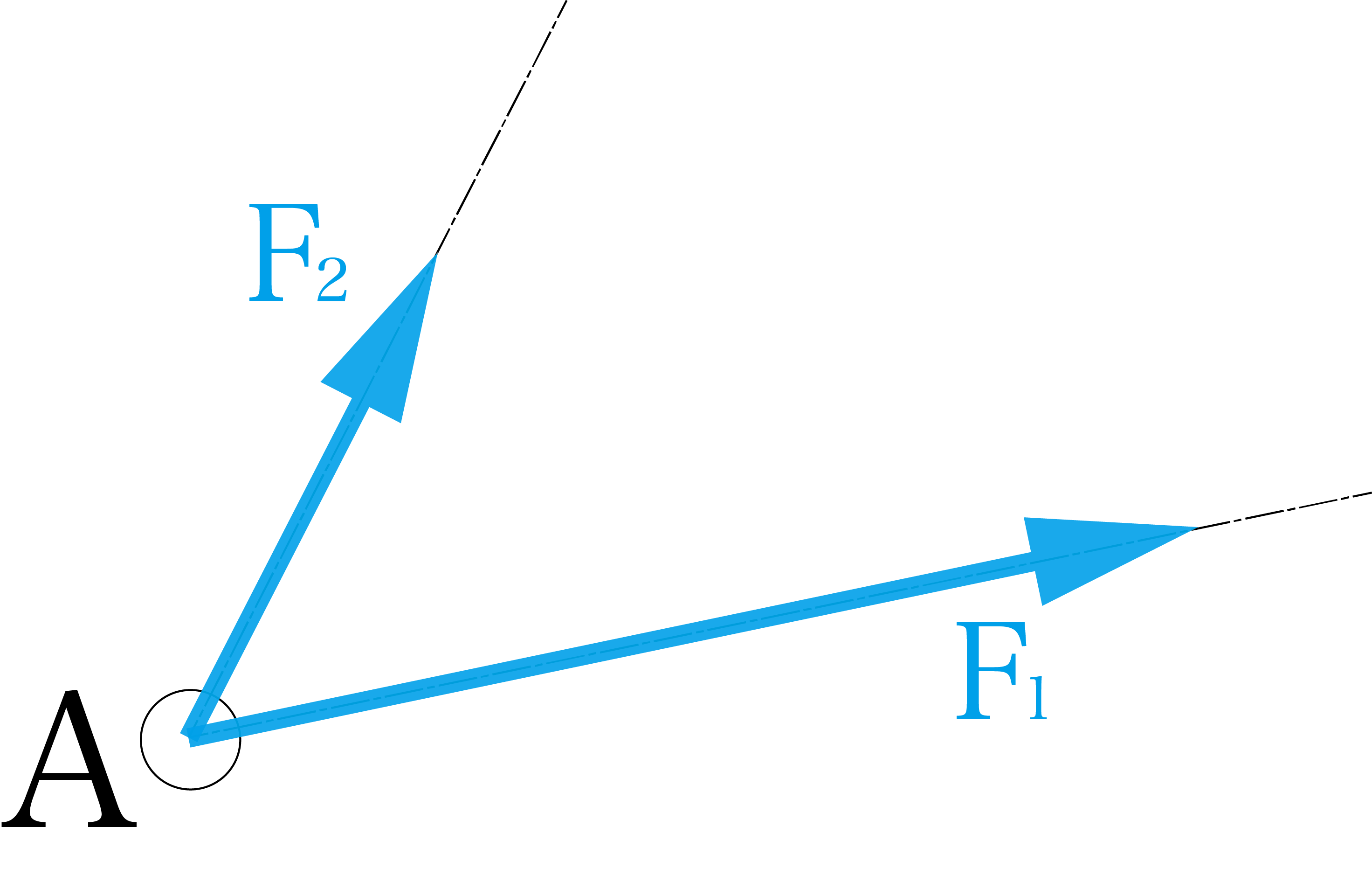
このように点Aに力F1とF2が働いていたとします。この2つの力を1つの力へ合成するにはどうすれば良いのでしょうか。2つの力を合成した結果は下の図のようになります。

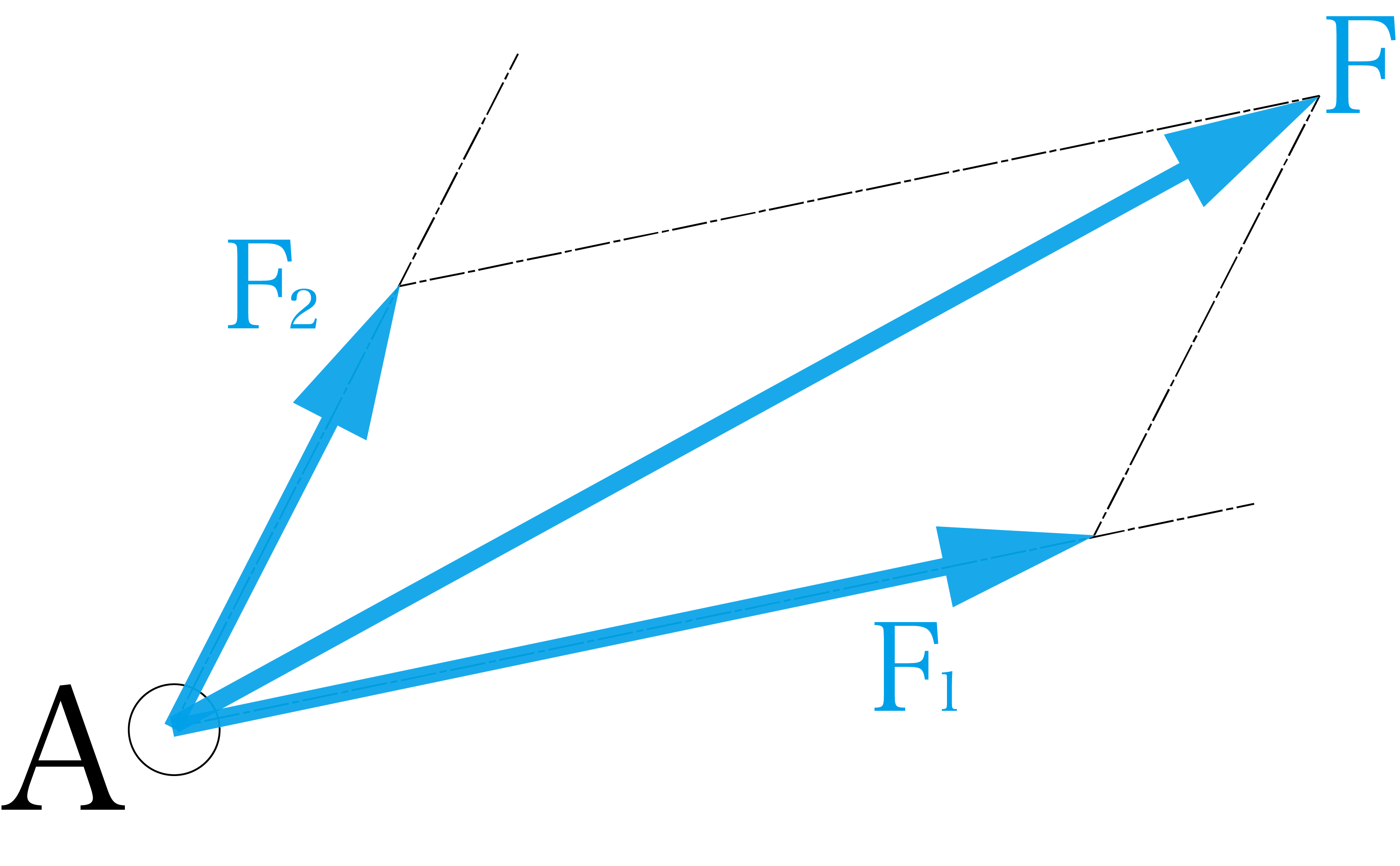
力の平行四辺形を作って、上の図のように対角線を結ぶと合成された力であるFとなるのでした。高校数学のベクトルと同じで、ベクトルの足し算と同じように力は合成されます。「力はベクトル！」と覚えておくと良いでしょう。

 

次に4つの力が働いている場合の力の合成を見てみましょう。

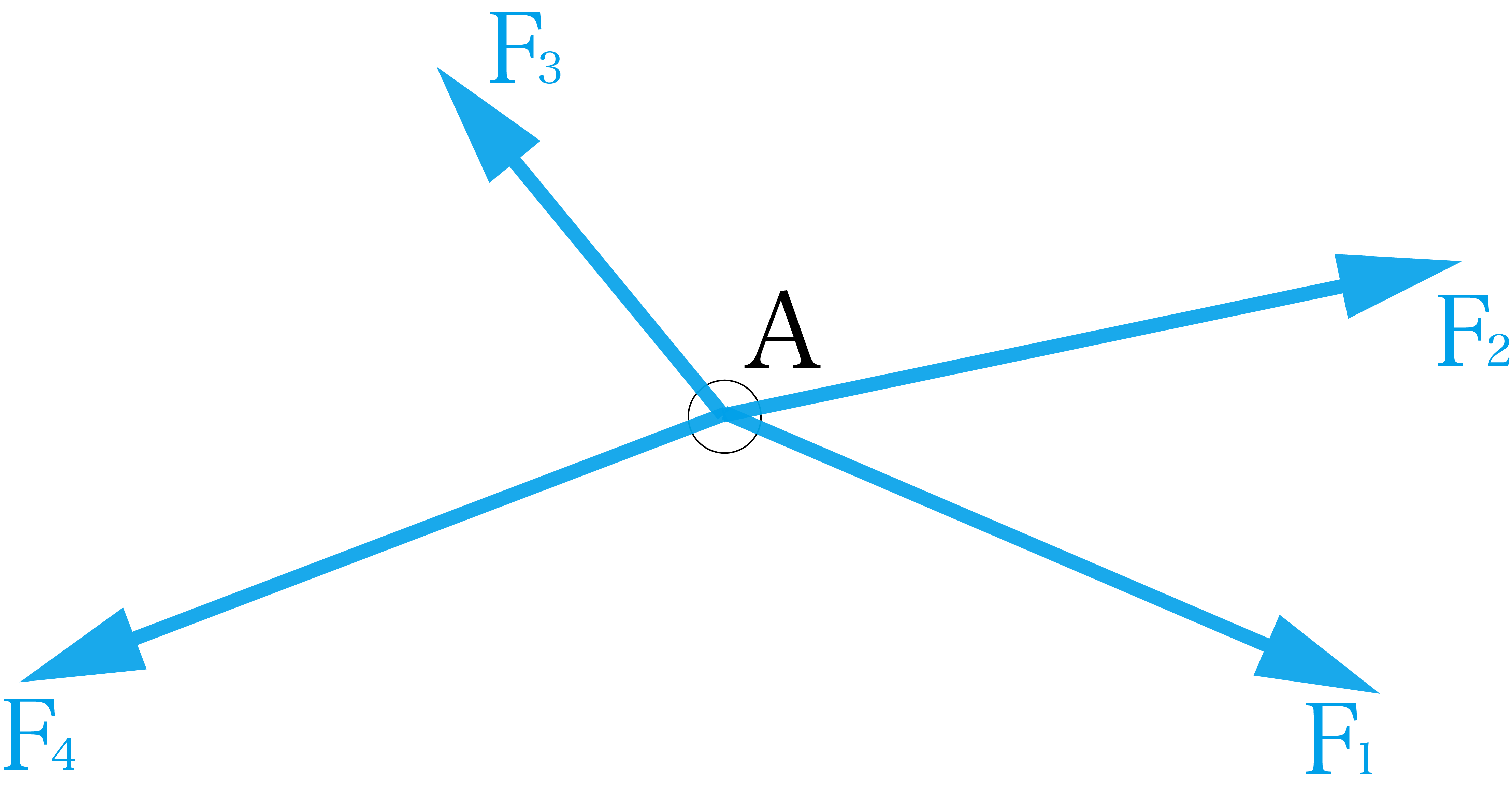
このように点Aに4つの力F1, F2, F3, F4が働いているとします。力はベクトルなので、これらの力を合成すると以下の図のようになります。

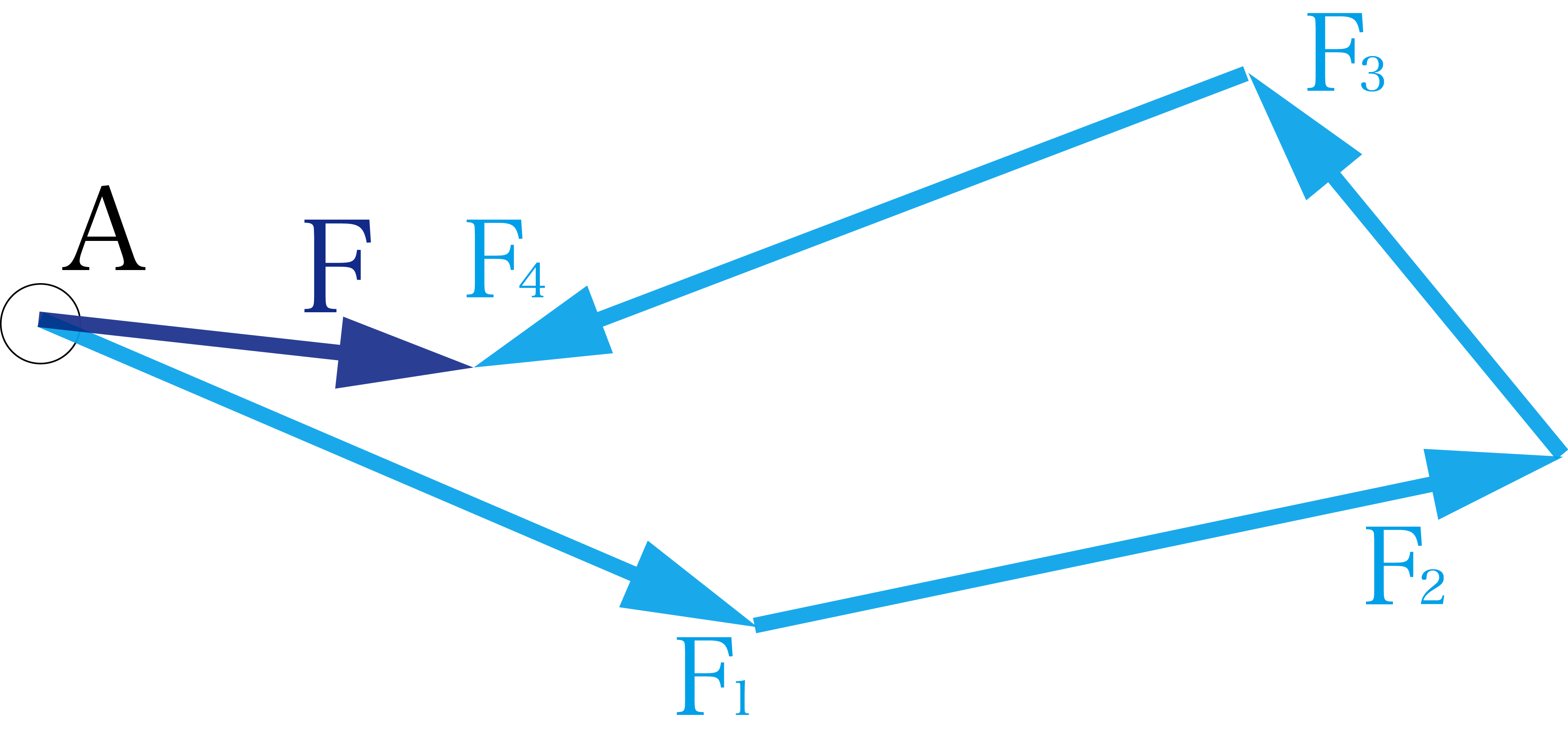
Fが合成力です。このように複数の力が働いている場合にも、ベクトルの足し算の要領で計算をしていけば力の合成は難しくありません。

 

力が釣り合う場合

上の例では合成力が発生するものを紹介しました。

次に力が釣り合う場合を考えてみましょう。下の図を見ていきます。

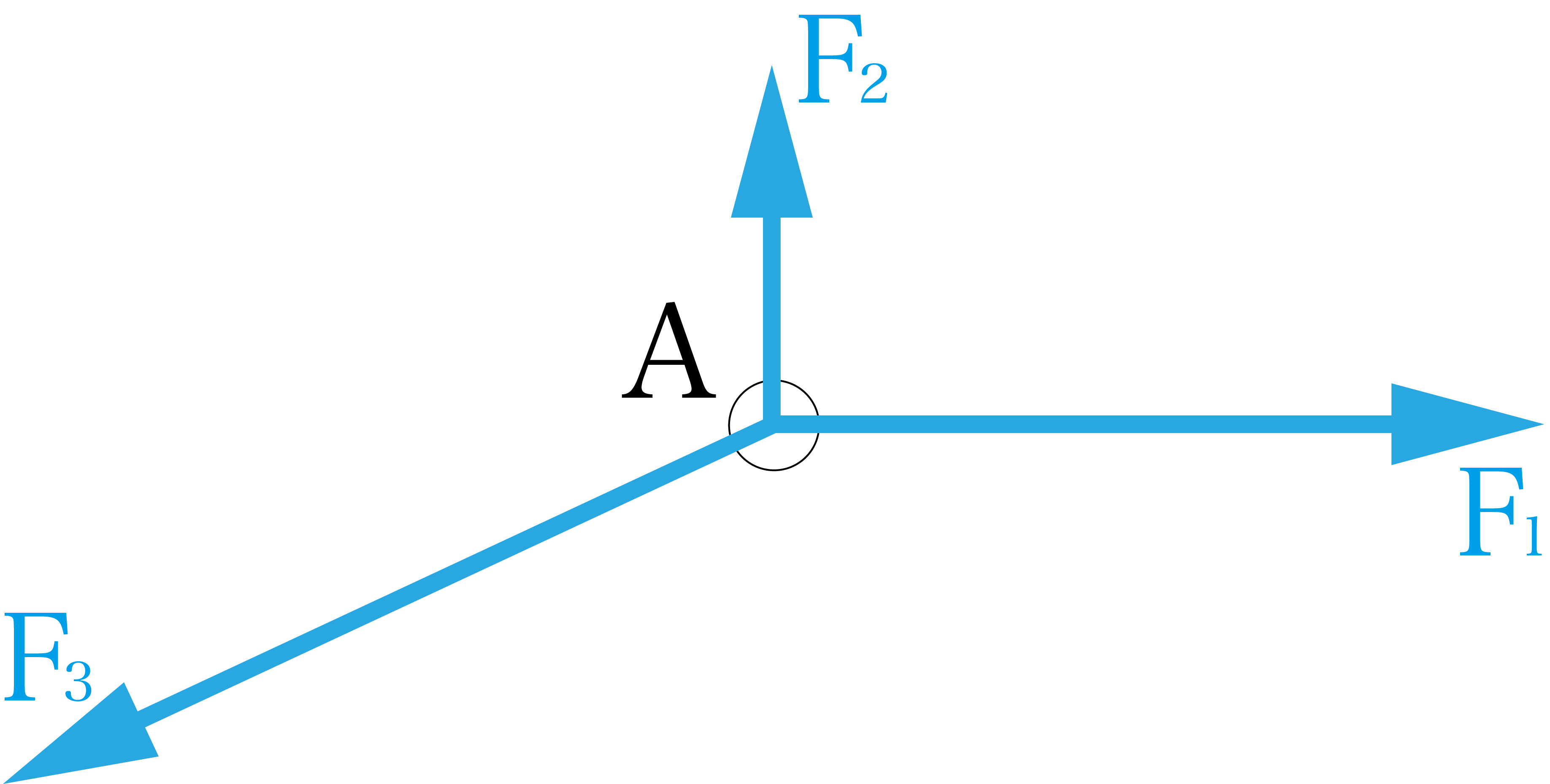
点Aに力F1, F2, F3が働いている場合です。これらの力を合成してみましょう。すると以下のようになります。

 

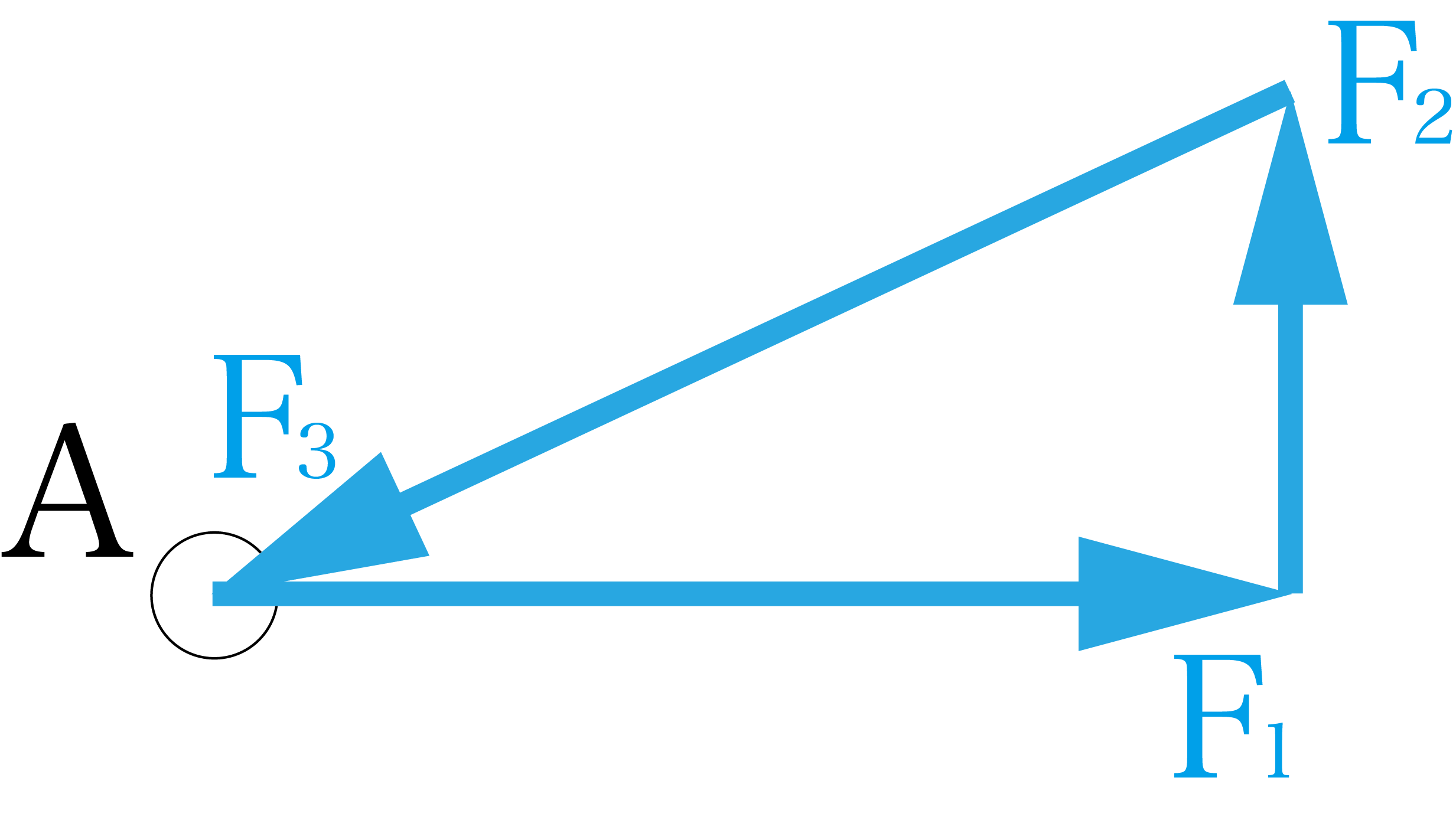
力の矢印の頭とお尻を合わせてベクトルの足し算をすると、F1のお尻とF3の頭がくっつきました。

この場合は合成力が発生しません。また、合成力が発生しない=力が釣り合っているということになります。実際に数値を計算せずとも、作図法から力が釣り合っていることがわかります。

 

力の分解の計算

さて、力の分解について説明していきましょう。

力の分解は力の合成の逆をすることです。力の合成では複数の力を1つにまとめていましたが、力の分解では1つの力を複数の分解に分けます。

実際に力の分解を考えていきましょう。次の図を見てください。

点Aにこのように力Fが働いていたとします。力の分解は基本斜めに働いている1つの力を水平方向(x軸方向)と鉛直方向(y軸方向)に分解します。そのため、力を分解した結果は次のようになります。

 

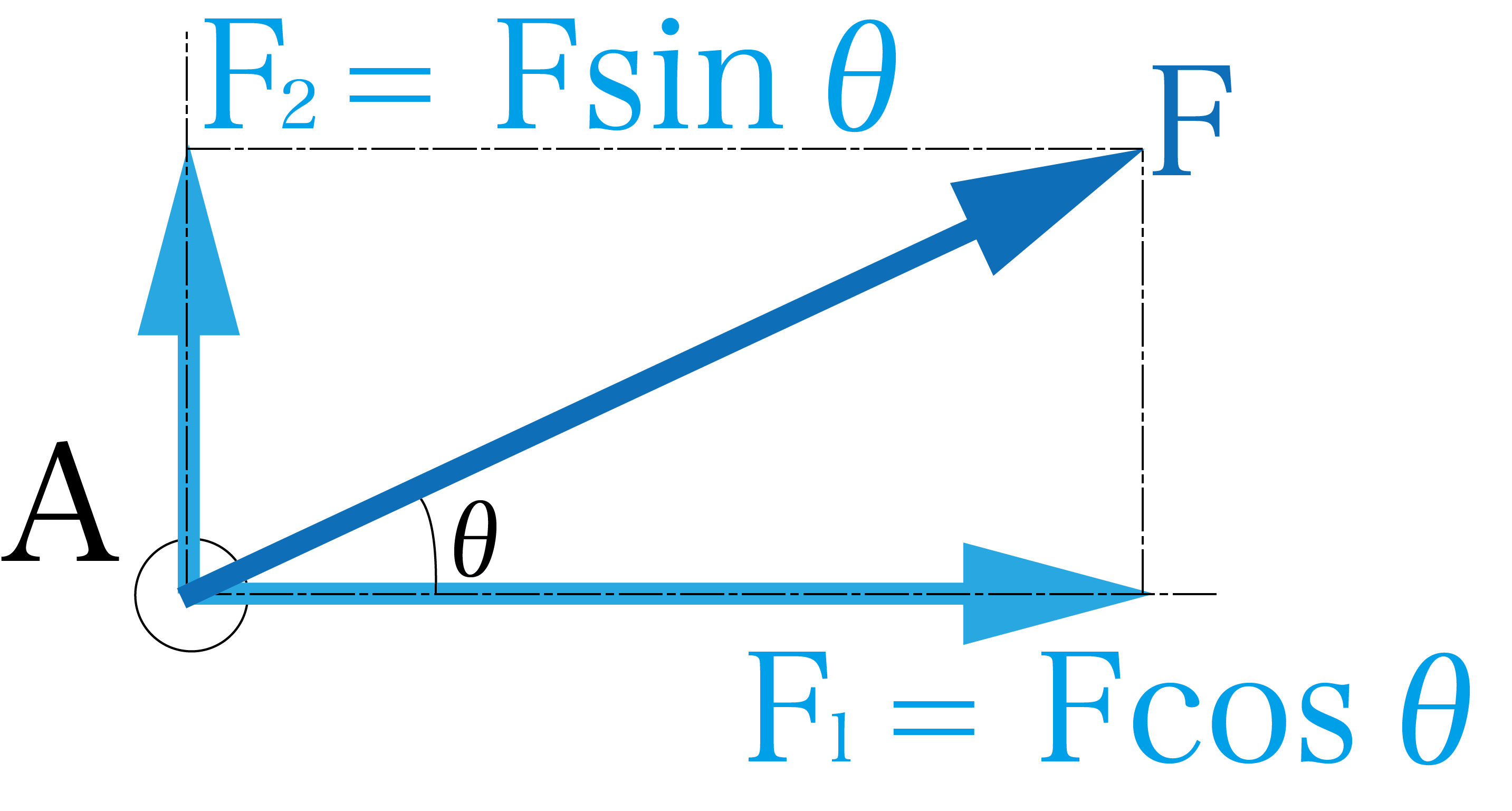
作図法で力の分解をすると、まずはじめにFの始点と終点を対角線とする長方形を作ります。そしてFの始点と長方形の水平方向の辺(F1)がFの水平成分、Fの始点と長方形の鉛直方向の辺(F2)がFの鉛直成分となります。これが作図法を用いた力の分解です。

数値を計算する場合は、水平成分はFにsinθをかけたもの、鉛直成分はFにsinθをかけたものになります。これは高校数学でも出てきた三角比を用いて計算します。そのため、鉛直方向とFのなす角θ(あるいは鉛直方向とFとのなす角)がわからないと、数値で力の分解をすることができません。

しかしだいたい問題として、なす角θは0[°]・30[°]・60[°]・90[°]のどれかに設定されていることが多いので、三角比を用いて力の分解をしましょう。

 

 

まとめ

今回は力の作図法の基礎となる、力の合成と力の分解について説明しました。力の合成と分解は高校数学のベクトルと三角比の知識を用います。そしてこれらは今後の作図解法で基礎となるものですので、しっかり理解するようにしてくださいね。

 

今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。