この記事では静定トラスと不静定トラスについて説明していきます。平面(2次元)で考えられるトラスにおける、静定トラスと不静定トラスとの違いについてまとめます。
静定トラスと不静定トラスの違いは、材料力学だけでなく建築構造力学を学んでいくにあたって欠かせない知識です。何度も復習をしながら理解を深めていってください。
それでは内容に入っていきましょう。
静定トラスとは?
まずはじめに静定トラスについてです。
静定トラスについて一言で説明すると、「静定トラスとは、全ての力の水平・垂直成分の和がゼロになり、任意の点における力のモーメントの合成がゼロになるトラス」です。しかし言葉で説明してもイメージがしづらいので、図を用いながら説明をしていきましょう。下の図をご覧ください。
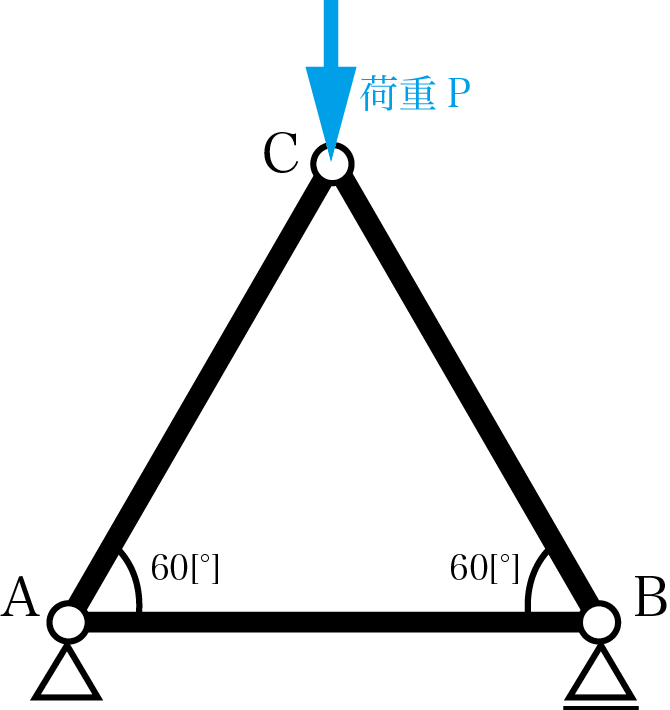
このようなトラスがあったとします。このトラスの各点における力の分解成分を求めてみましょう。
静定トラスの力の各成分を求める
この静定トラスには荷重が働いているので、下の2つの支点から支点反力が働きます。支点反力を図に書き入れると以下のようになります。
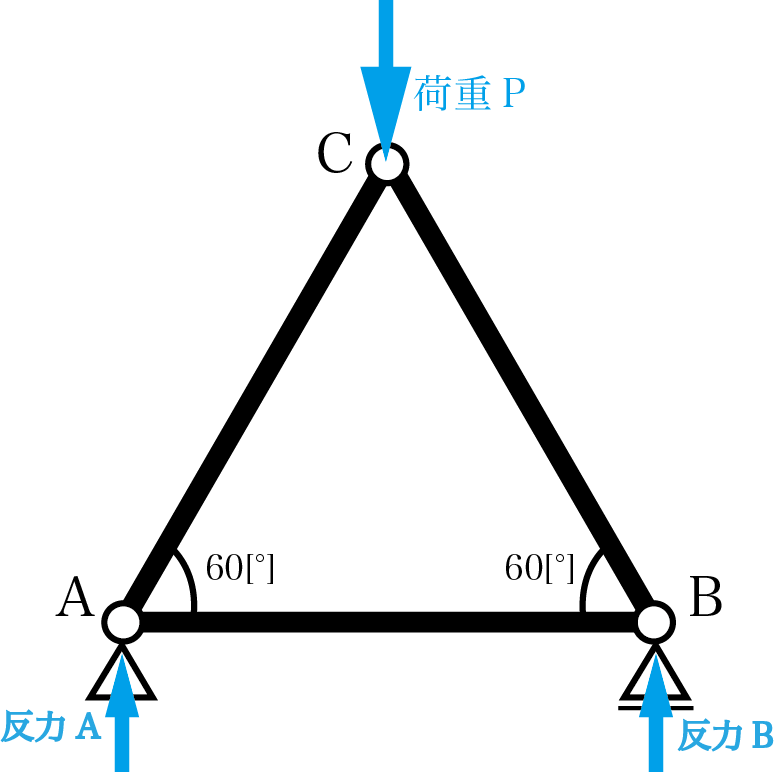
正三角形のトラスなので、反力A=反力Bであり、それらの和は荷重Pと等しくなります。
しかし部材ACと部材BCは水平方向から60[°]傾いていますので、反力がそのまま荷重に伝わるわけではありません。そのため、部材内でどのように力が伝わっているかを考える必要があります。そこで、力の分解を利用して、部材内でどのように力が荷重に反しているかを考えていきます。
今回は正三角形のトラスなので、力の分布は左右対称です。よって、支点A側の力の分布だけを計算しましょう。
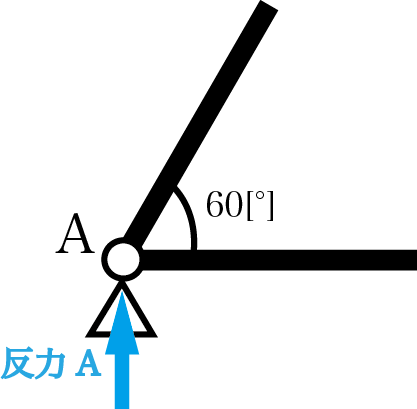
支点Aを拡大した図が上です。反力Aを分解して、水平方向と水平から60[°]傾いた2つの成分にします。

反力Aを水平方向成分(分解反力Ab)と水平から60[°]傾いた成分(分解反力Ac)の2つに分解すると、上の図のようになります。今回は細かい数値の計算は省略するので、イメージだけ抑えてください。数値の計算は演習問題で紹介しますので、そちらを参照してください。
部材に沿って水平方向と水平から60[°]傾いた2つの成分に分解したので、支点Aには上の図のように力が働くと考えられます。部材方向と、水平左方向に力が働きます。
これと左右対称にしたものが、支点B側でも発生しています。
次に支点C側でどのようになっているかを考えます。
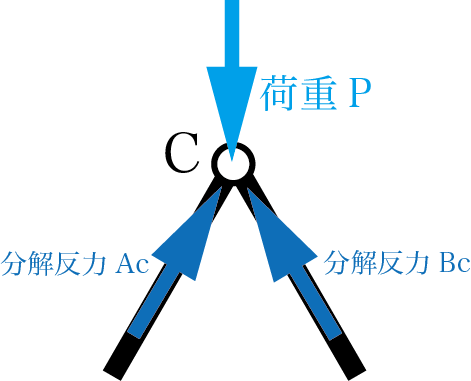
支点Cを拡大すると、このように力が働いていることがわかります。分解反力AcとBcの垂直成分が荷重Pと釣り合うということになります。また、AcとBcの大きさが等しいため、それぞれを水平成分に分解するとそれらが釣り合います。
今回力の数値の計算はしていませんが、この例で紹介したトラスは全ての節点で閉じた三角形ができています。このような場合は全ての水平成分と垂直成分の和がゼロになり、これを静定トラスと呼びます。
不静定トラスとは?静定トラスとの違いは?
さて、静定トラスについての説明が終わったところで、次に不静定トラスについて説明しましょう。
不静定トラスについて簡単にいうと、「静定トラスでないトラス」です。もう少し厳格な意味での不静定トラスを説明しましょう。
静定トラスに関しては、トラスの部材に軸力(部材の向きに沿った内力)だけが生じると考えて、全ての節点の力の釣り合いから、トラス全体の力の釣り合いを考えました。
節点以外に力が作用して、部材に曲げせん断力が生じたり、節点で部材の変形を考えなければならない場合は、力の釣り合いだけでは解くことができません。このようなトラスを不静定トラスと呼びます。
静定トラスと不静定トラスの違いについて
ここまで静定トラスと不静定トラスについてそれぞれを説明しましたので、違いはわかっていただけたかと思います。
静定トラスと不静定トラスの違いは、単純に力の釣り合いだけで解けるか解けないかです。これだけ覚えておけば、違いについては簡単にわかるでしょう。
まとめ
今回は静定トラスと不静定トラスについて紹介しました。
静定トラストは、トラス全体の力の釣り合いが、各節点の力の釣り合いから求めることができるものでした。逆に不静定トラスは曲げやせん断力が発生するため、力の釣り合いだけでは全体に力がどのように伝わっているかを求めることができないトラスです。これらをしっかり理解した上で、今後の学習に役立ててください。
今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。
