この記事では断面二次極モーメントと極断面係数に関して解説をしていきます。この記事を読むと、断面二次極モーメントと、極断面係数についての基礎を理解することができます。
断面二次極モーメントと、極断面係数に関しては、基礎となる断面二次モーメントと断面係数について知っていると、理解が早くなります。断面二次モーメントと断面係数に関しては以前まとめた記事がありますので、理解が進んでいない場合は是非読んでください。
断面二次モーメントとは?計算方法は?導出過程についても紹介!
断面二次モーメントも断面係数も建築材料力学の分野では非常に重要な概念です。さて、今回は梁の変形と強さを求める断面二次モーメントと断面係数のように、軸についての変形と強さを求めるための係数を考えます。
断面二次極モーメントと極断面係数の公式の導出
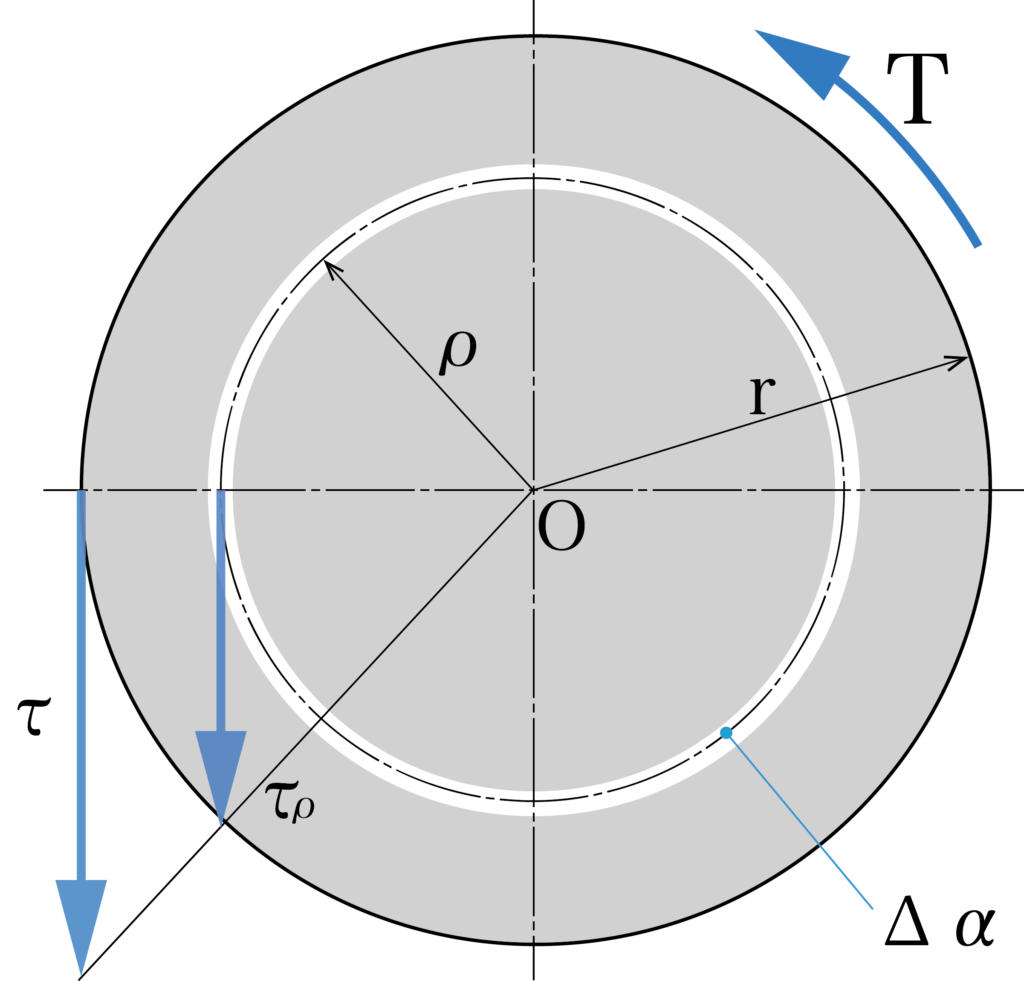
半径rの軸がねじりモーメントTを受けて表皮に最大ねじり応力τが発生しているとしましょう。この軸の中心軸と垂直な断面に、半径ρの同心円で演習の微笑面積Δaのリングを考えます。この部分にねじり応力τρが発生するとします。ねじりモーメントTとねじり応力τの関係を考えていきましょう。
ここからは計算式を紹介しながら説明して行くので、実際に紙とペンで手を動かしながら読んでいってください。
・半径ρにおけるねじり応力τρ
τ : τρ = r : ρ
∴τρ = τ × ρ/r
・微小面積Δαに生じる内力ΔF’
ΔF’ = τρΔα = τ × ρ/r × Δα
・ΔF’が点Oに及ぼすモーメントΔT’
ΔT’ = ΔF’ρ = τ × ρ²/r × Δα
断面全体に生まれるモーメントをT’とすれば、T’は軸に与えられたねじりモーメントTと大きさが等しく逆向きなので、T’ = Tとして下の式が成り立ちます。
T’ = ΣΔT’ = Σ(τ×ρ²/r × Δα) = τ/r × Σρ²Δα = T
ここで、Σρ²Δαは断面の形状で決まる値なので、Σρ²Δα = Ipとすると、下の式が導出されます。
T = τ/r × Ip
また、Ip/rも断面形状で一定値を持つので、Ip/r = Zpとして、下の式が導かれます。
T = τZp
Ipを断面二次極モーメント、Zpを極断面係数と呼びます。これらを公式としてまとめると、以下のようになります。
Ip = T × r/τ
Zp = T / τ
(Ip:断面二次極モーメント、T:ねじりモーメント、r:半径、τ:ねじり応力、Zp:極断面係数)
断面二次極モーメントと極断面係数の値について
次に断面二次極モーメントと極断面係数の値について説明していきます。
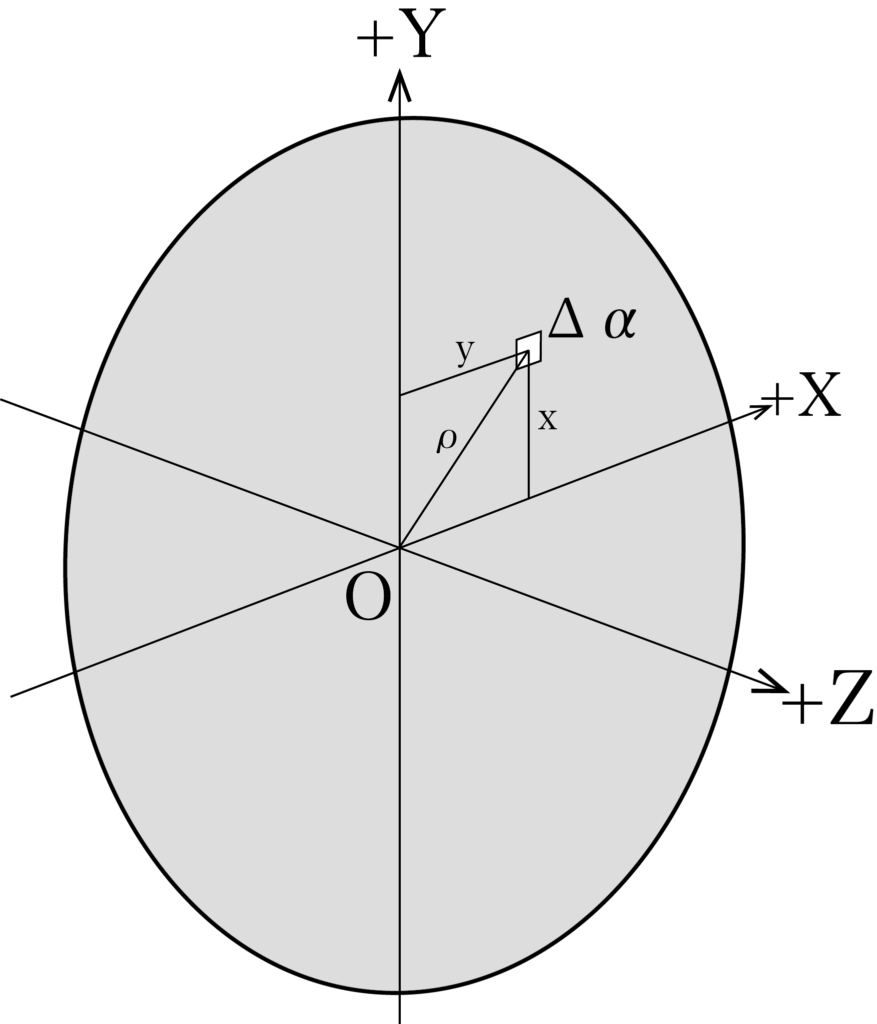
X-Y-Zの直交座標で、物体の断面をX-Y平面におき、断面状に原点からの距離ρにある微小面積Δaを考えます。すると、上で説明したようなρ²Δaは、Z軸に対する断面二次モーメントとなり、これを断面二次極モーメントIpと呼ぶのでした。ここで、ρ²=x²+y²なので、IpはX軸とY軸に対する断面二次モーメントの和に等しくなります。
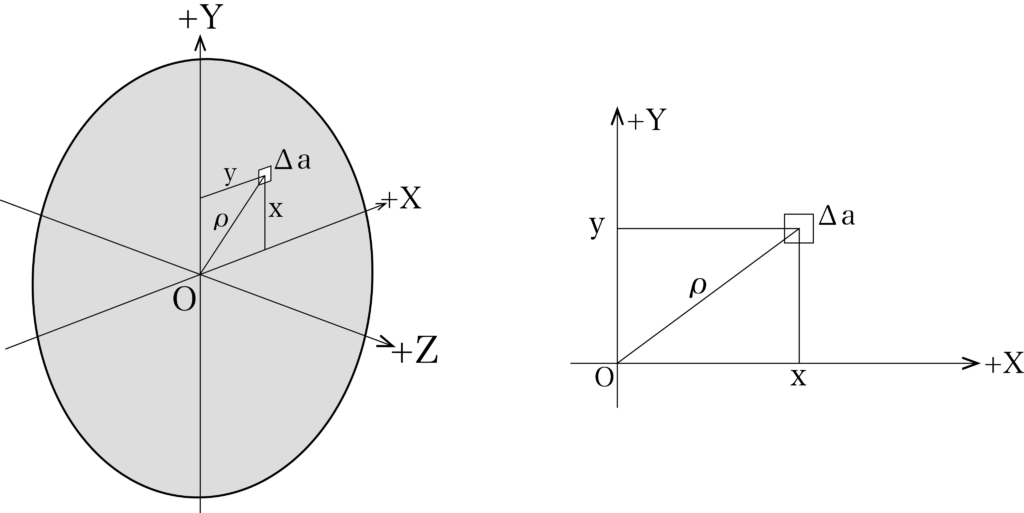
断面X-Yにおける、断面二次極モーメントの計算をしていきましょう。
Ip = Σρ²Δa = Σ(x²+y²)Δa = Σx²Δa + Σy²Δa = Ix + Iy
この式から、断面X-Yにおける断面二次極モーメントは、X軸とY軸に対する断面二次モーメントの和となります。
円形断面ではIx=Iyなので、Ix=Iy=Iとして、Ip=Ix+Iy=2Iというように表すことができます。中実円形(空洞のない円形)軸の直径をdとして、断面二次極モーメントと極断面係数は以下のように表されます。
断面二次極モーメントIP = 2I = 2 × π/64 × d⁴ = π/32 × d⁴
極断面係数ZP = Ip/r = 2/d × π/32 × d⁴ = π/16 × d³
円形軸で一般に使われる断面二次極モーメントと極断面係数の算出式を表にまとめます。
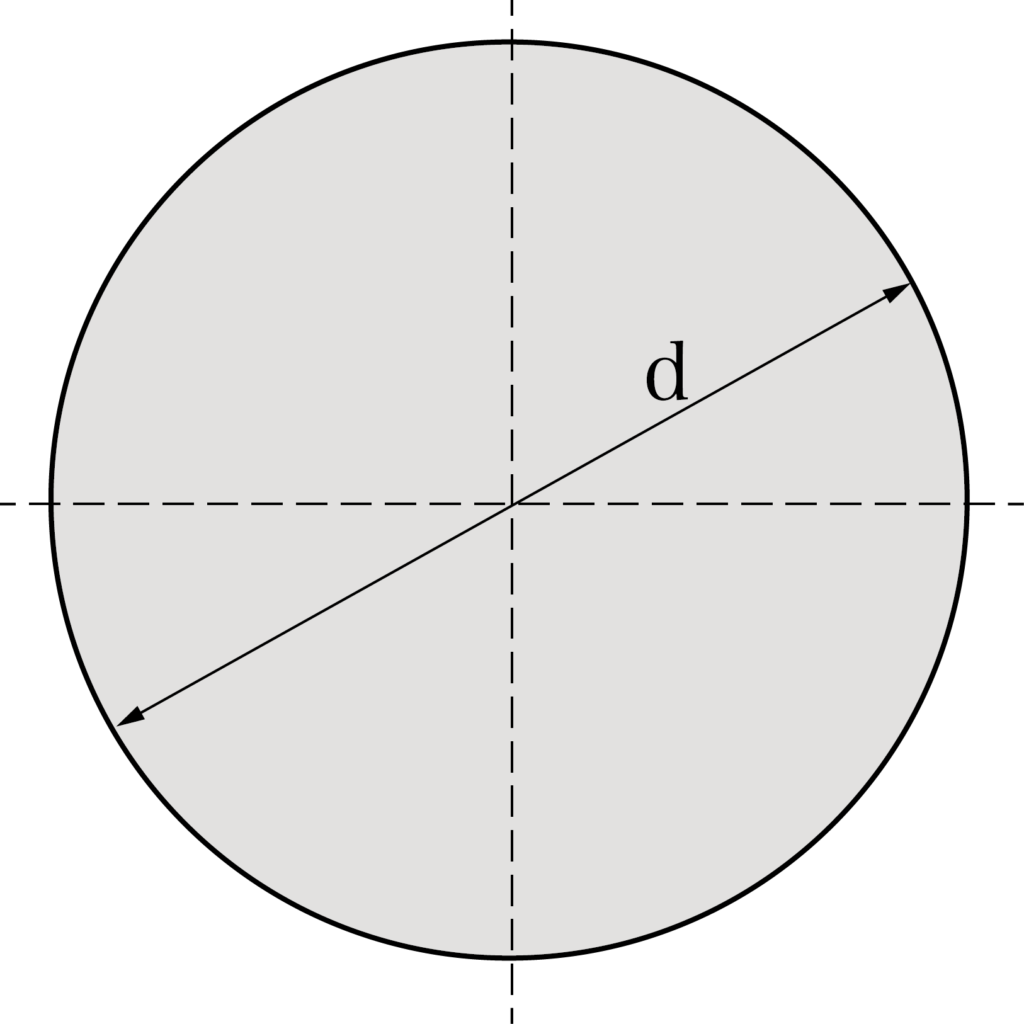
断面二次極モーメントIP = π/32 × d⁴
極断面係数ZP = π/16 × d³
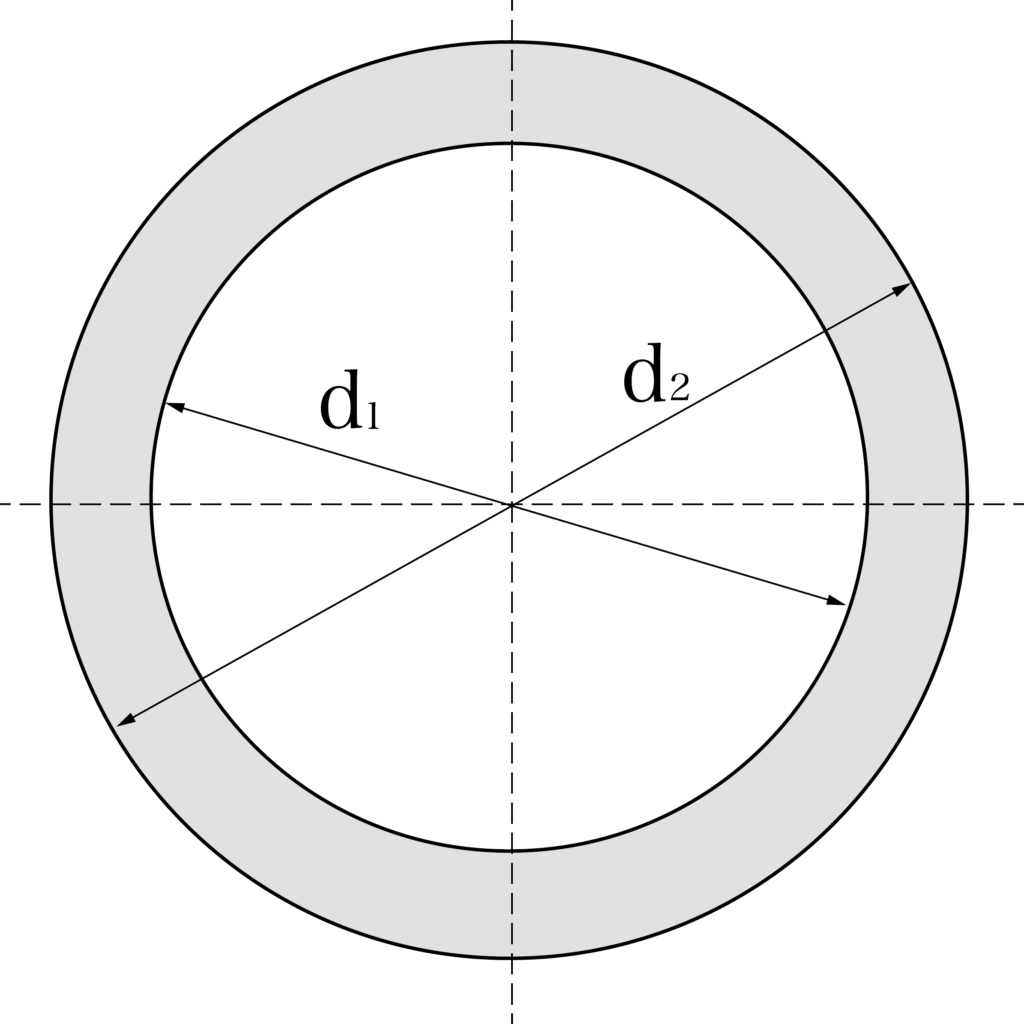
断面二次極モーメントIP = π/32 × (d1⁴ – d2⁴)
極断面係数ZP = π/16 × (d1⁴ – d2⁴)/d2⁴
まとめ
今回は断面二次極モーメントと極断面係数について紹介しました。断面二次モーメントと断面係数について理解をしていれば、今回の記事の理解も簡単だったのではないでしょうか。ぜひ理解を深めて、これからの勉強に役立てていってくださいね。
今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。