材料力学の仕事・仕事率(動力)・トルクについて

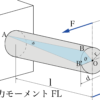
今回は伝道軸に関しての基礎を紹介していく記事になります。

回転することで動力を伝達する軸を伝道軸と呼びます。

軸のねじりモーメントと仕事や、動力の関係について考えていきましょう。

それでは早速内容に入っていきます。

 

 

仕事・動力・トルク

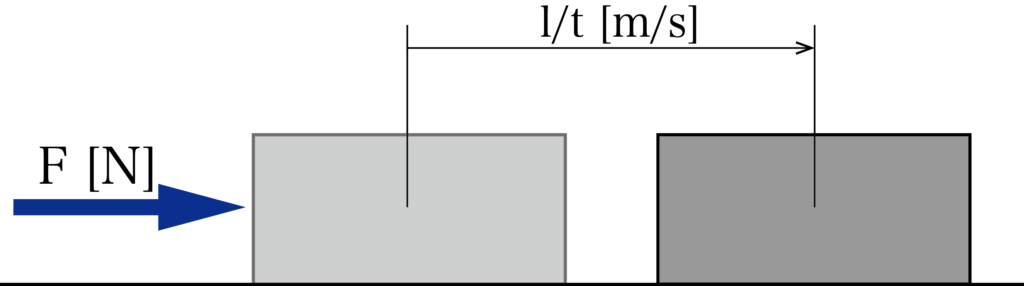
物体が力F[N]を受けて時間t[s]で力の向きに距離l[m]移動したとしましょう。

この時、F×lを仕事W(単位[J])と呼びました。

また、この仕事を仕事のかかった時間t[s]で割った値を仕事率P(単位[W])あるいは動力と呼びます。

ここまでは高校物理の範囲なので、わかる人が多いでしょう。

 

機械のエンジンやモーターなど、回転軸のねじりモーメントを一般にトルクと呼びます。

トルクに関しては以前まとめた記事がありますので、こちらを参照してください。

機械分野では実務的に、1分間あたりの回転数をNで表します。

回転軸の仕事率(動力)・トルク・回転数を関連させた式を考えます。

 

それでは仕事と仕事率、トルクの式を実際に見ていきましょう。

これは高校物理の力学の分野ですでに勉強しているはずなので、復習として紹介しました。

 

さて、次に大学の物理で初めて登場する”トルク”に関しての式を見ていきましょう。

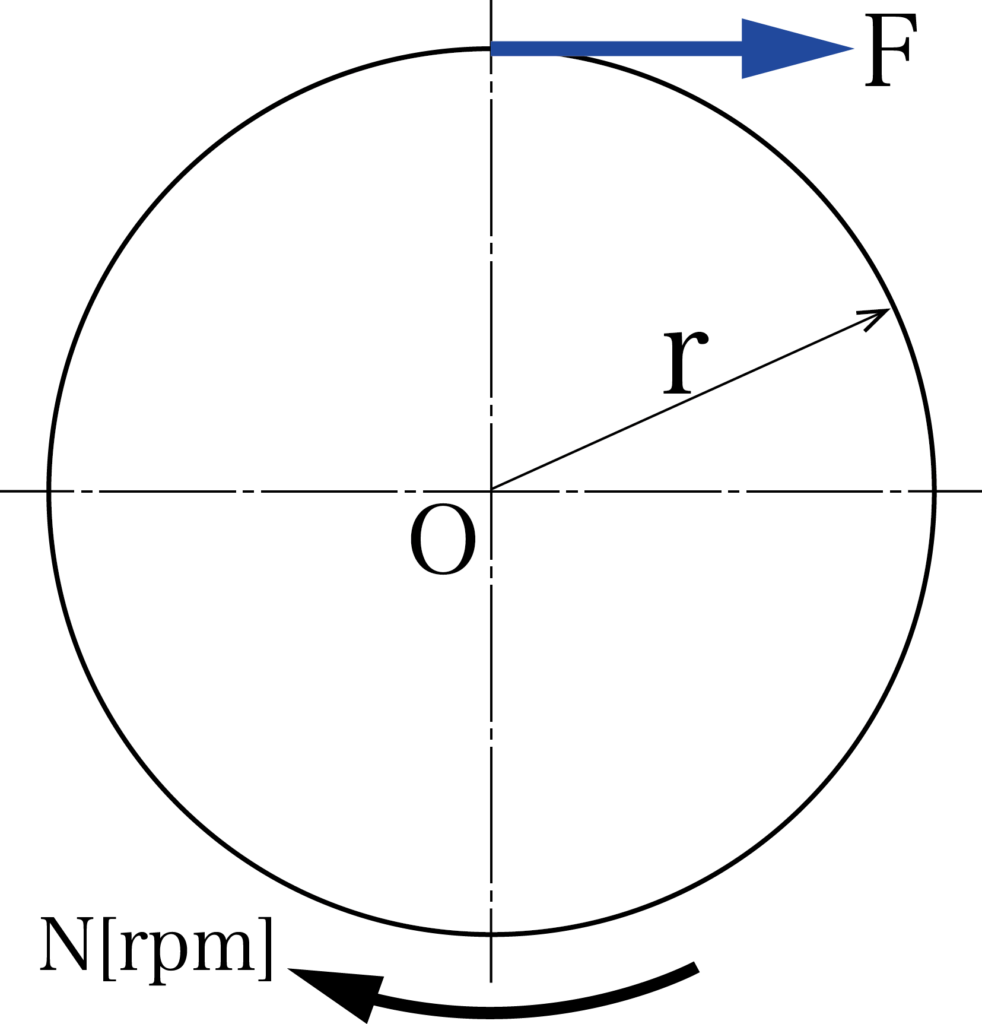
原点Oに対するトルク=力×半径で求めることができるので、

T = F × r(T：トルク[N・mm]、F：力[N]、r：半径[mm])

となります。

 

ここで、半径rの円が1分間にN回転して得る距離lは、円周×N(=2πrN)と等しくなりますので、1分間あたりの軸のする仕事は、以下のように表すことができます。

W = F × l = F × 2πrN × 10^(-3) = 2πTN × 10^(-3)

(W：仕事[J]、F：力[N]、l：距離[m]、T：トルク[N・m]、N：回転数)

ここで、10^(-3)は、単位を[mm]から[m]に変換するために掛けています。

 

軸の仕事率(動力)、1分=60秒の換算(1/60倍)で計算していきます。

P = W / t = {2πTN×10^(-3)} / 60 = 2πTN / 60×10^(-3)

(P：仕事率、t：時間)

この式から分かるように、仕事率(動力)Pは、トルクTと回転数Nの積に比例します。

 

 

仕事・仕事率・トルクの例題を紹介

ではここまで紹介した仕事や仕事率、トルクに関しての概念を、実際に計算をして確認していきましょう。

 

例題1：トルクを求める問題

300[rpm]で5[kW]の動力(仕事率)を伝達している軸に生じるトルクを求めなさい。

 

解答例

解答を見ていく前に、単位の[rpm]に関して少し触れておきましょう。

rpmとはrevolution per minuteの略であり、回転数のことを表します。

回転数はただの”数”なので、一般的には単位はありません。

しかし回転数であることをわかりやすくするために、[rpm]として表しました。

 

それでは解答を見ていきましょう。

上の式で紹介した通り、動力(仕事率)P=2πTN / 60×10^(-3)でした。

この式を使って答えであるトルクを求めていきます。

T = P×60×10³/2πN = 5×10³×60×10³/(2π×300) = 1.59×10⁵[N・mm]

 

答え

トルク：1.59×10⁵[N・mm]

 

 

例題2：動力(仕事率)を求める問題

500[rpm]で回転する直径40[mm]の軸の許容ねじり応力を50[MPa]とする。

伝達できる最大動力(仕事率)を求めなさい。

 

解答例

では解答例を見ていきます。

トルクの式は以下の公式から導くことができます。

この式から、

T = τZpを導出することができます。

 

また、中軸円形軸(空洞のない円形軸)の極断面係数は以下の式で求めることができます。

極断面係数Zp = π/16 × d³

これらを組み合わせて式を作り、答えを求めていきましょう。

T = τZp、Zp = π/16 × d³より

T = τ × π/16 × d³

 

次にトルクと回転数から動力(仕事率)を求めます。

動力(仕事率)P = 2πTN / 60×10^(-3) = 2πN / 60×10^(-3) × (τ×π/16×d³)

= (2π × 500× 50 × 40³) / (60×10³ × 16)

= 32.9 × 10³[W]

 

答え

動力(仕事率)：32.9 × 10³[W]

 

 

まとめ

今回は仕事や仕事率(動力)、トルクについてまとめました。

仕事や仕事率については高校物理でも出てきたものですが、トルクは大学で初めて登場する概念でした。

また、材料力学では仕事率のことを動力と呼ぶこともありますので、これも合わせて覚えておきましょう。

 

今回の記事は以上になります。

最後まで読んでいただき、ありがとうございました。