この記事では、軸のねじれと軸の断面の関係について書いていきましょう。
回転することで動力を伝達する軸のことを伝動軸と呼びます。
モーターなどはその例としてイメージしやすいでしょう。
今回はこの伝動軸についてを考えていきましょう。
中実円形軸の動力とねじれ
まず初めにトルクと断面形状の関係を考えていきます。
トルクとは、ねじりモーメントのことを指します。
ねじりモーメントはその名の通り、ねじりを発生させるモーメントのことですが、材料力学のような機械工学の分野では、ねじりモーメントをトルクと呼びます。
このトルクと断面形状の二つの関係についてを、ねじり応力、トルク、ねじれ角などの基本式から導出していきましょう。
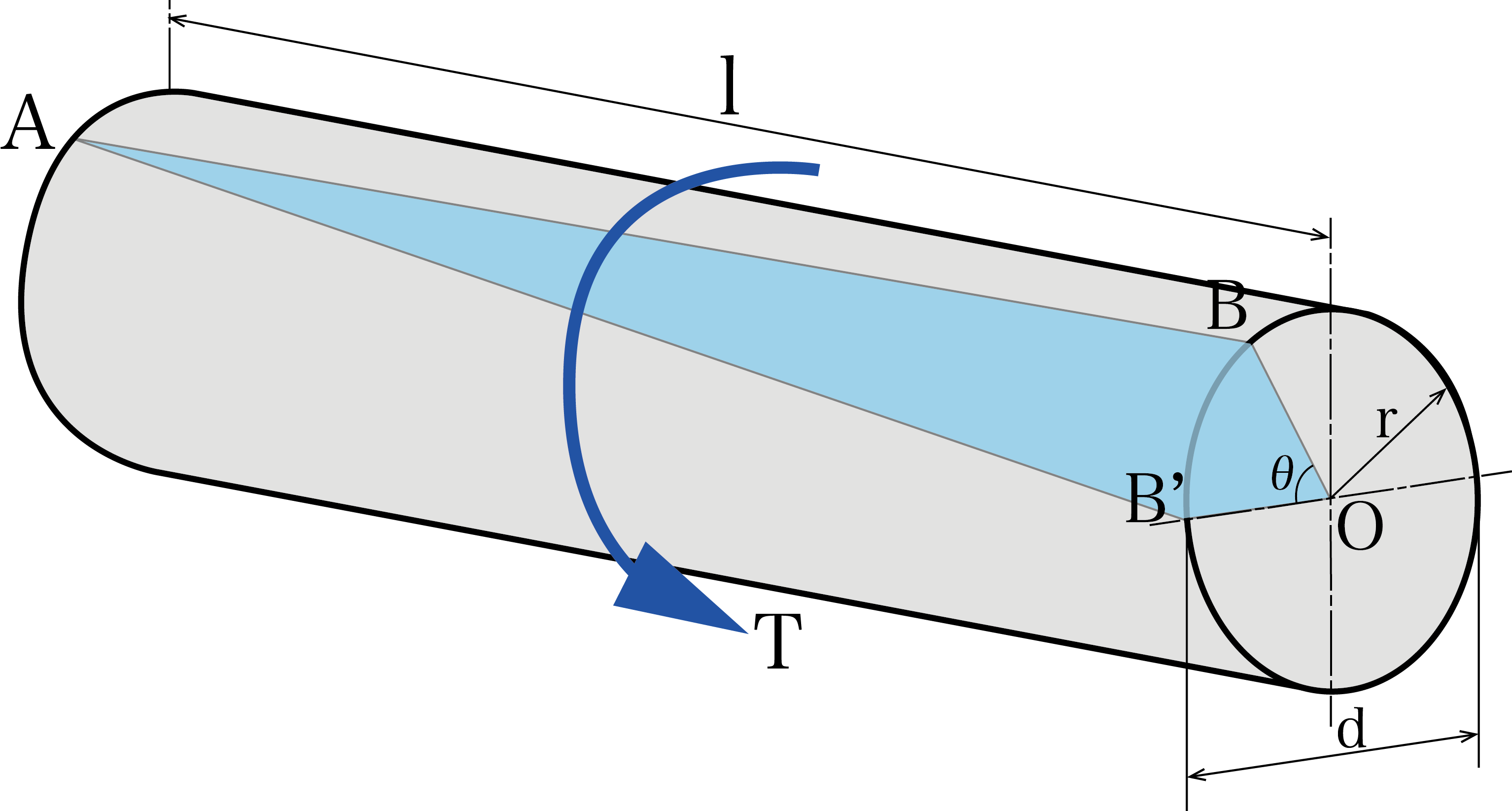
ねじれ角θを初めに求めていきます。
ねじり応力τ = Gγ、せん断ひずみγ = rθ / l
∴ ねじれ角θ = τl/Gr …(1)
次にねじり応力τを求めていきます。
トルクT = τZp、極断面係数Zp = π/16 × d³
∴ ねじり応力τ = 16T/πd³ …(2)
式(2)を式(1)に代入して、τを消去します。
半径r = d/2として計算をしていきます。
ねじれ角θ = τl/Gr = 16T/πd³ × l/Gr = 16T/πd³ × l/G × 2/d
= l/G × 32T/πd⁴ …(3)
ここで、断面二次極モーメントを考えます。
断面二次極モーメントについては以前解説した記事がありますので、知りたい方は参考にしてみてください。
さて、中実円形軸の断面二次極モーメントの公式は以下のようなものでした。
Ip = πd⁴/32 …(4)
式(4)のIp = πd⁴/32を、式(3)のθ = l/G × 32T/πd⁴に代入して、直径dを消去します。
θ = Tl / GIp …(5)
この式に含まれるGIpは、この値が大きくなることによってねじれ角θが小さくなりますので、ねじり変形に対する抵抗の度合いを表すねじり剛性と呼ばれます。
まとめ
今回は伝動軸のねじれについて紹介しました。
公式というよりも、軸のねじれと軸の断面の関係を断面二次極モーメントから求める過程を解説してきました。
このように公式を覚える以外にも、式の組み合わせからあるものとあるものの関係を導き出すのは非常に大切です。
今回の記事を参考にしながら、勉強に役立てていってくださいね。
この記事は以上になります。
最後まで読んでいただき、ありがとうございました。
