今回は少し発展的な因習問題を取り上げていきましょう。

今回取り上げる問題は計算量が結構多いので、読むだけではなく実際に紙とペンを動かしながら考えていってください。

 

 

演習問題：熱を受ける組み合わせ部材の問題

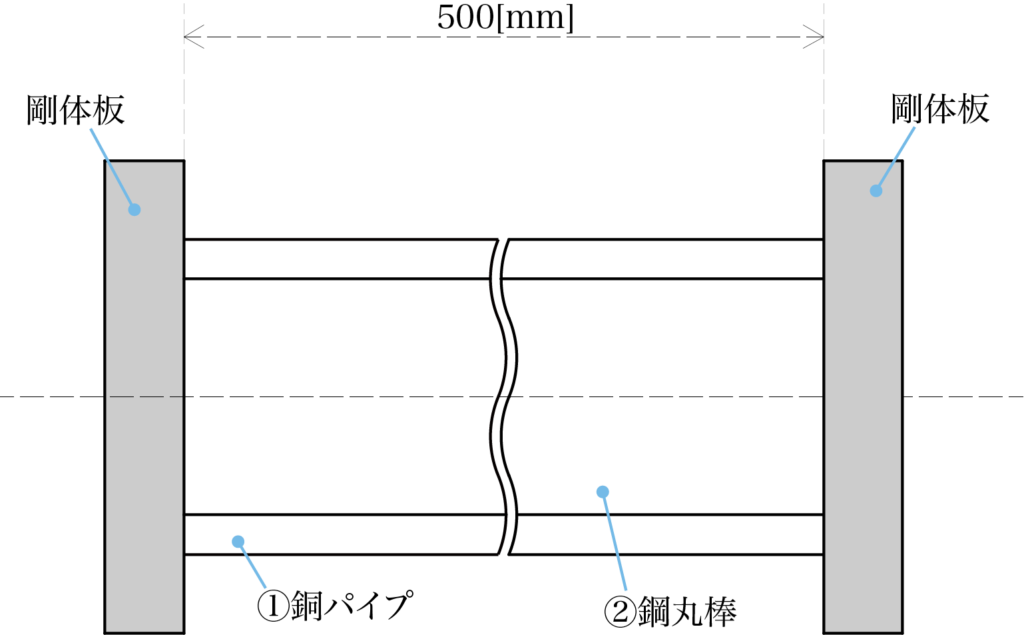
温度20[℃]で、①銅パイプと②鋼丸棒の両端を剛体板で固定して組み合わせた長さ500[mm]の部材がある。

全体の温度が100[℃]になった時①と②に生じる応力を求めなさい。

①と②の材質の諸元を表に示します。

image

 

 

▽①銅パイプと②鋼丸棒の諸元

①銅 ②鋼
断面積(mm²) A1 = 5000 A2 = 3000
縦弾性係数(GPa) E1 = 100 E2 = 206
線膨張係数(×10^(-6)/K) α1 = 17.6 α2 = 11.5




 

解答例

最初に考え方から紹介していきます。

①銅パイプと②鋼丸棒は固定されていますから、変形量が等しいことを頭に入れておく必要があります。

今回はまず文字で計算をしてから最後に数値を代入して値を出していきます。

 

それではまず変形量から求めていきましょう。

①銅パイプの変形量は以下の式で与えられます。

変形量λ = ①銅パイプの自由変形量λ1 + 拘束量λ1‘

 

②鋼丸棒の変形量は以下の式で与えられます。

変形量λ = ②鋼丸棒の自由変形量λ2 + 拘束量λ2‘

 

①銅パイプと②鋼丸棒の変形量は必ず等しくなりますから、これを式に表すと

λ1 + λ1‘ = λ2 + λ2‘…(1)

になります。

 

次にそれぞれの自由変形料を求めましょう。

熱ひずみの公式は以下のようなものでしたね。

熱ひずみの公式

ε = αΔt

(ε：熱ひずみ、α：線膨張係数、Δt：温度変化)

ひずみεは、λ/l(変形量/元の長さ)で与えられるものでしたので、それを代入すると下のような式に変形できます。

λ / l = αΔt

→ λ = αlΔt

これを使って自由変形量を求めます。

λ1 = α1lΔt、λ2 = α2lΔt…(2)

 

 

応力とひずみを関係は以下の公式で与えられましたね。

応力とひずみの関係式

ε = λ / l = σ / E

→ λ = σl / E

 

これを使ってそれぞれの変形量λ’を求めていきましょう。

λ1‘ = σ1l / E1、λ2‘ = σ2l / E2…(3)

 

式(1)に式(2)と式(3)を代入して整理をします。

λ1 + λ1‘ = α1lΔt + σ1l / E1、λ2 + λ2‘= α2lΔt + σ2l / E2

式(1)のλ1 + λ1‘= λ2 + λ2‘より、

α1lΔt + σ1l / E1 = α2lΔt + σ2l / E2

lが共通しているので、両辺をlで割ると、

α1Δt + σ1 / E1 = α2Δt + σ2 / E2…(4)

 

①銅パイプの軸力と②鋼丸棒の軸力は釣り合うので、下の式が成り立ちます。

応力σ = P/Aより、P = σAが成り立つので、

σ1A1 + σ2A2 = 0

→σ2 = -σ1A1 / A2…(5)

 

式(5)を式(4)に代入してσ2を消去してσ1を求めます。

式(4)：α1Δt + σ1 / E1 = α2Δt + σ2 / E2

式(5)：σ2 = -σ1A1 / A2

α1Δt + σ1 / E1 = α2Δt + -σ1A1 / E2A2

上の式を整理してσ1を求める式に変形します。

 

σ1を左辺に移行します。

σ1A1/E2A2 + σ1/E1 = α2Δt – α1Δt

次に同類項を整理しましょう。

σ1(A1/E2A2 + 1/E1) = Δt(α2 – α1)

σ1{(E1A1+E2A2) / E1E2A2} = Δt(α2 – α1)

 

以上の式をσ1=の形に直すと、

σ1 = E1E2A2Δt(α2 – α1) / (E1A1+E2A2)…(6)

 

σ1の式は出ましたので、式(6)を式(5)に代入してσ2を求める式を作ります。

式(5)：σ2 = -σ1A1 / A2

式(6)：σ1 = E1E2A2Δt(α2 – α1) / (E1A1+E2A2)

 

σ2 = –E1E2A2Δt(α2 – α1)A1 / (E1A1+E2A2)A2

= –E1E2Δt(α2 – α1)A1 / (E1A1+E2A2)…(7)

 

 

σ1とσ2を求める式が完成したので、最後に数値を代入して答えの値を求めていきましょう。

σ1 = E1E2A2Δt(α2 – α1) / (E1A1+E2A2)

= -{100×10³ × 206×10³ × 3000 × (100-20) × (11.5-17.6)×10^(-6)} / {100×10³ × 5000 + 206×10³ × 3000}

= -27.0[MPa]

答えの符号がマイナスなので、σ1は圧縮応力であることを示しています。

 

σ2 = –E1E2Δt(α2 – α1)A1 / (E1A1+E2A2)

= -{100×10³ × 206×10³ × 5000 × (100-20) × (11.5-17.6)×10^(-6)} / {100×10³ × 5000 + 206×10³ × 3000}

= 45.0[MPa]

答えの符号がプラスなので、σ2は引張応力であることを示しています。




 

答え

①銅パイプに生じる応力；圧縮応力27.0[MPa]

②鋼丸棒に生じる応力；引張応力45.0[MPa]

 

 

まとめ

今回は少し計算量の多い難しめの問題を取り扱いました。

計算量は確かに多いのですが、材料にどんな作用がかかるのかを考えてしっかりと公式通りに解いていけばちゃんと答えは出せる問題です。

おそらく大学の試験や建築士試験にもこのような問題は出ると予想されますから、難しめですがしっかりと理解しておきたいところですね。

なんども復習をして、マスターしておきましょう。

 

今回の記事は以上になります。

最後まで読んでいただき、ありがとうございました。