材料の変形や応力の原因となるものには、主に外力があります。これは最もイメージがしやすい事柄で、外力を受けた材料が変形するところは想像しやすいでしょう。
しかし材料の変形や応力の原因となるものは外力だけではありません。温度変換も材料に変化をもたらします。温度変化が材料に与える影響について、今回の記事では紹介していきます。
線膨張係数(熱膨張率)の計算方法は?熱ひずみとの関係は?
熱ひずみの説明をする前に、知識として知っておかなければならない線膨張係数(熱膨張率)について紹介していきましょう。
材料は温度が上昇すれば膨張します。また、温度が低下すると収縮します。このように材料の温度が変化することによって、材料の体積変化が起こります。
線膨張係数αとは、材料の軸方向に変化する度合いを、単位温度あたりのひずみで表したものです。
ではその計算方法について説明していきましょう。
線膨張係数は常に一定の数値ではないため、あある温度範囲の平均値で表します。材料の線膨張係数(熱膨張率)αは、以下のように定義されています。
α = (1/l) × (Δl/Δt)
(l:物体の長さ Δl:長さの変化量 t:物体の温度 Δt:温度の変化量)
一般的に、物体の線膨張系数αはごく小さな値となります。
材料の線膨張係数について、いくつか具体的な数値例を表で紹介します。
| 材料 | 線膨張係数α
[10^(-6)/K] |
| 鋼 | 11.3 ~ 11.6 |
| ステンレス鋼 | 9.0 ~ 17.3 |
| 鋳鉄 | 9.2 ~ 11.8 |
| アルミニウム | 23.6 |
さてここでは線膨張系数とその計算方法について紹介しましたが、次は本題の熱ひずみに入っていきましょう。
熱ひずみとは?計算方法や対策は?
熱ひずみの概念について紹介していきましょう。熱ひずみとは、その名の通り温度変化によって生じたひずみのことです。
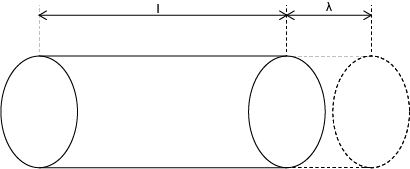
上の図を参照してみましょう。棒状の材料は、体積変化のほとんどが長さの変化になります。床に置いた長さlの棒材が、温度t1からt2への温度変化(t2 – t1 = Δt)を受けると、線膨張係数αを比例定数としてΔtに比例した変形量λが生まれます。このλをlで割った値を熱ひずみεと呼びます。
熱ひずみを求める式を紹介すると、以下のようになります。
ε = λ / l
= αlΔt / l
= αΔt
(α:線膨張係数、λ:変形量、l:材料の元の長さ、Δt:温度変化)
変形量λ = αlΔt
温度変化Δt = t2 – t1
(t1:変化前の温度、t2:変化後の温度)
まとめ
今回は熱ひずみの概念を説明しました。また、熱ひずみを説明するために必要な線膨張係数に関しても紹介しました。
ひずみとは元の長さと変化量の割合を表すものでしたが、熱ひずみも基本的に考え方は変わりません。材料に発生するひずみの原因は、外力によるものが多くそのイメージが強いと思いますが、材料に変形を促すのは外力だけではありませんでした。温度変化によって材料の体積変化が起こるので、それによってもひずみは発生するのでしたね。材料の変形は外力と温度変化によるものがあるということを覚えておきましょう。
今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。


熱ひずみの分母はなぜ、自由膨張後L(1+αΔT)ではなく、膨張前Lなのですか?
定義ではなく、理由が知りたいです。調べた限りのどの教科書も同じ定義だが、理由が書いてない。仮に、定義したとしても、もし実際に発生する熱応力が計算値と異なる場合は、定義自体が間違いとなるはず。熱膨張が微小とだからと仮定するのも、膨張量次第では、前者と後者の値が大きくずれてしまうから成り立たないと思われる。
カジカさん
コメントありがとうございます。
>>熱ひずみの分母はなぜ、自由膨張後L(1+αΔT)ではなく、膨張前Lなのですか?
>>定義ではなく、理由が知りたいです。
ひずみの定義は「λ/L(λ:材料の変形量、L:材料の元々の長さ)」です。
熱ひずみも温度変化で発生するひずみですので、こちらの定義に従って分母は膨張前の材料の長さLとなります。