今回は熱応力の例題を紹介していきます。
材料の変形をもたらすのは外力だけではありません。
材料の変形を考える時に一番イメージしやすいのは外力によるもの出るが、材料は温度変化をすることによって体積変化が起きるので、それによっても変形します。
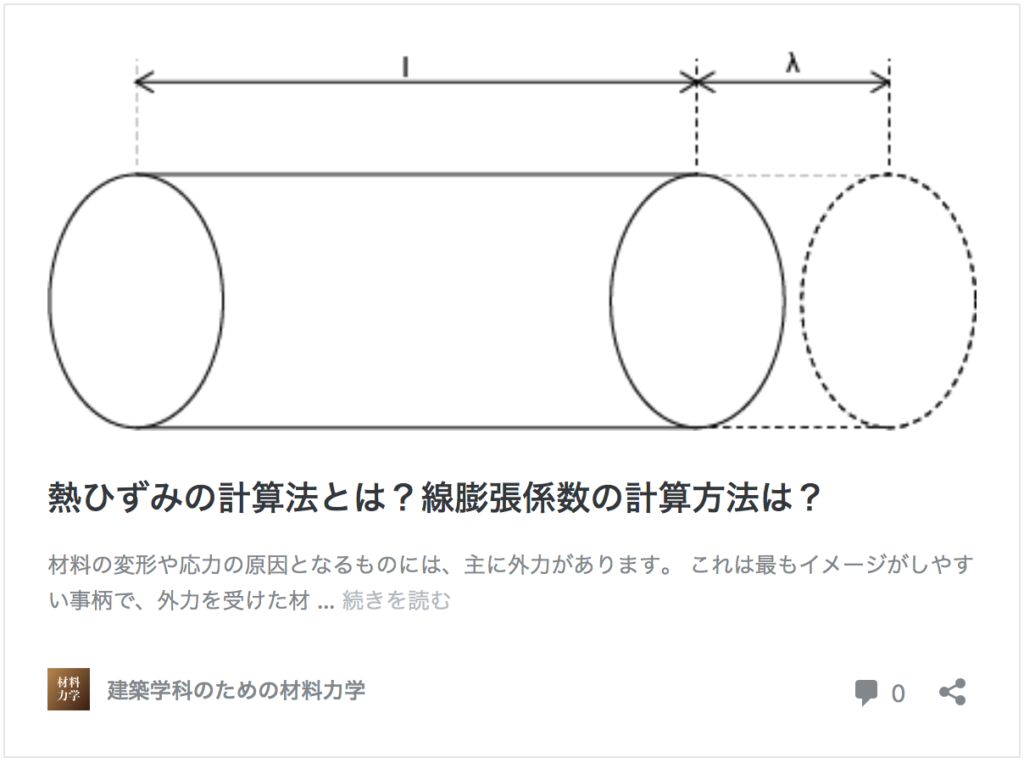
熱によって発生する材料のひずみを熱ひずみと呼ぶのでした。
また、材料に発生する熱ひずみがどれくらいの値になるかを計算するのに線膨張係数という係数が存在するのでしたね。
この熱ひずみ、線膨張係数に関しては、下の記事で詳しくまとめています。
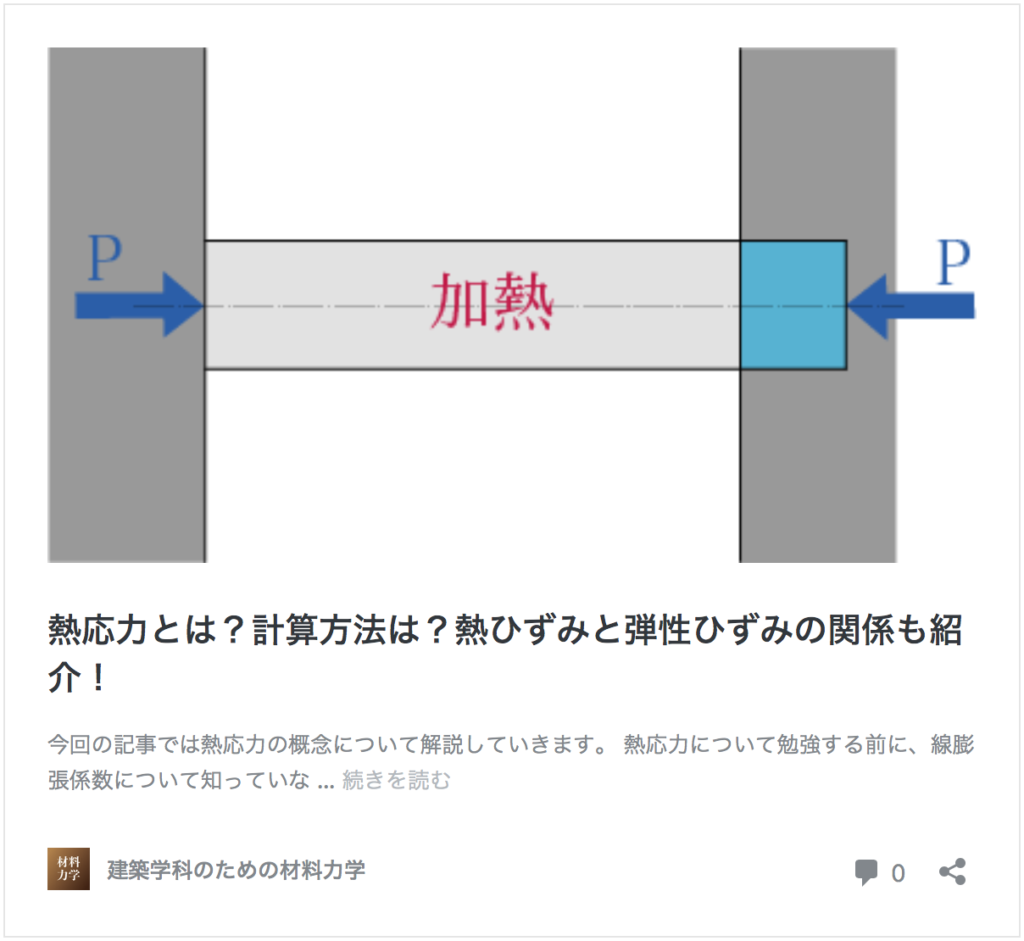
また、材料が固定されている場合は材料に温度変化が起きた場合でも体積変化ができません。
その場合には熱応力という応力を考えるのでしたね。
今回の演習問題では熱応力の概念も出てきますので、熱応力に関してまだ知らない人は下の記事を読んでください。
では早速演習問題に入っていきましょう。
演習問題:伸縮する軸の応力
間隔を固定した2つの剛体壁がある。伸縮できる段付き軸の一方を壁から通し、他端を固定した。温度300[℃]のとき首した長さ1[m]で壁と1[mm]の隙間をもつ。軸の温度が200[℃]になったとい、軸はどうなるかを答えなさい。材料の縦弾性係数を206[GPa]、線膨張係数を11.5×10^(-6)[/K]とします。
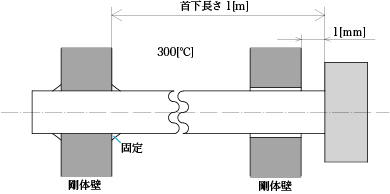
解答例
まず考え方から書いていきましょう。
収縮量が1[mm]になるときの温度t2を求めます。
次にt2が200[℃]に達しない場合は、さらに収縮し熱応力が発生します。
そこで、t2から200[℃]までの垂直応力を求めます。
では最初に収縮量が1[mm]の時の温度t2を求めましょう。
変形量を求める式は以下で与えられました。
変形量λ = αl(t2 = t1)
この式を変形して、t2を求めていきます。
t2 = t1 + λ/αl
= 300 + (-1)/(11.5×10^(-6) × 1×10³) ←分子の(-1)は伸びを正・収縮を負としている
= 213[℃]
上の計算から、1[mm]収縮した時の温度が200[℃]に達しないので、t2=213[℃]からt3=200[℃]までの温度変化における熱応力を考えます。
熱応力の式は以下の公式で与えられましたね。
熱応力σ = -EαΔt
(σ:熱応力、E:縦弾性係数(ヤング率)、α:線膨張係数、Δt:温度差)
この公式を用いて計算していきます。
熱応力σ = -EαΔt
= -Eα(t3 – t2)
= -206×10³ × 11.5×10^(-6) × (200 – 213)
= 30.8[MPa]
それでは最後に解答をまとめます。
答え
軸の収縮は拘束(固定)され、30.8[MPa]の引張応力が発生する。
まとめ
今回は熱による材料の変形の問題を取り扱いました。
温度変化によって材料は体積変化を起こしますから、それによる変形を考慮しなければなりません。
また、温度変化による材料の変形の問題には今回の演習問題の他にも、関連記事に関連問題を載せてあるので、「ほかの問題も解いてみたい!」という人はぜひ挑戦してみてください。
今回の記事は以上になります。
最後まで読んでいただき、ありがとうございました。
今日も勉強お疲れ様です。