熱ひずみ・熱応力の例題！計算方法は？演習問題を紹介！

今回は熱によって材料に変化が生じる場合の問題を解いてみましょう。

 

材料に変化をもたらすのは外力だけではありません。

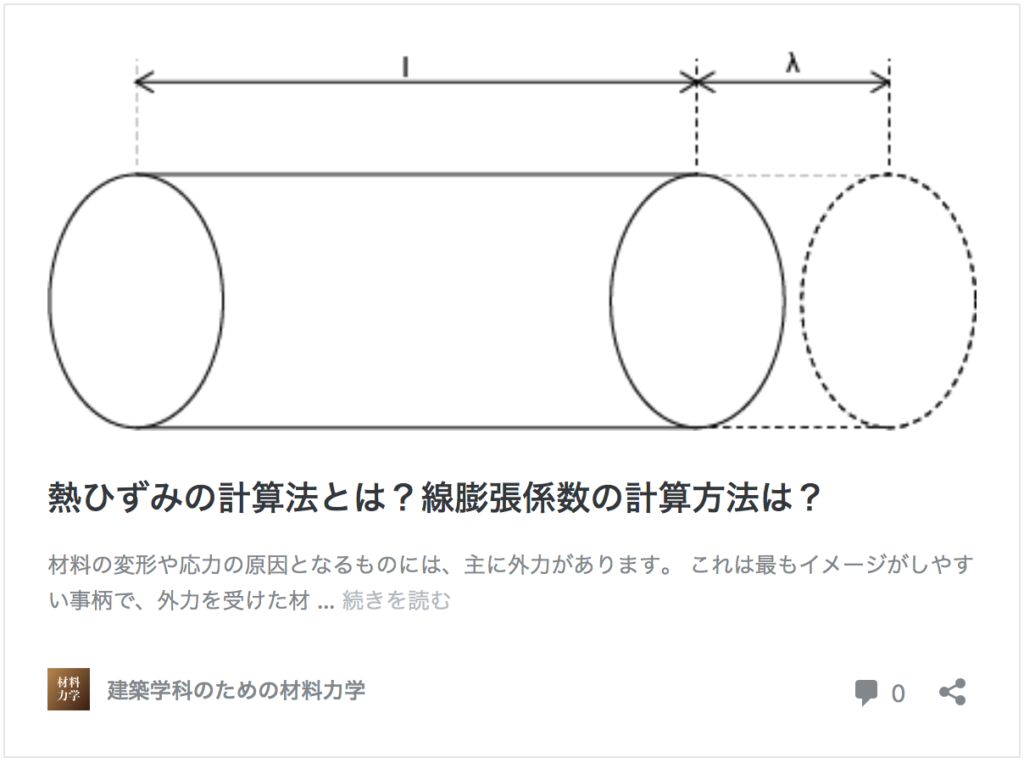
材料の変形を考える時に一番想像しやすいのは外力によるものですが、材料は温度変化することによっても変形します。

熱による材料のひずみを熱ひずみというのでしたね。

また、材料の熱ひずみがどれくらいかを計算するのに線膨張係数という値があります。

これに関しては下の記事で解説しているので、まだ熱ひずみと線膨張係数について知らない方は下の記事を読んでから問題を解くようにしましょう。

 

演習問題：鉄道用レールの伸縮

鉄道のレールは、温度変化によるレールの伸縮対策として、レールの継ぎ目に遊間と呼ぶ隙間を設けています。

長さ25[m]の定借レールが温度45[℃]の時、隙間がゼロで接しているとします。

レールの伸縮は自由として、レールの温度が-5[℃]の時の遊間とレールの温度が55[℃]の時のレールに発生する応力を求めなさい。

材料の縦弾性係数を206[GPa]、線膨張係数を11.5×10^(-6)[/K]とします。

 

 

解答例

 

熱ひずみは上の公式で求められました。

最初にこの公式を変形して、変形量であるλを求める式にします。

λ/l = αlΔt/l

→ λ = αlΔt

この式を用いて、レールの温度が-5[℃]の時の遊間を求めていきましょう。

 

問題にあるレールの長さは25[m]ですが、単位を[mm]になおして計算します。

また、温度変化はそのままの温度を代入して求めていきます。

変形量λ = αlΔt

= αl(t2 – t1)

= 11.5×10^(-6) × 25×10³ × (-5-45)

= -14.4

答えの符号がマイナスになっていますが、これはレールの収縮量を表しています。

レールが収縮すると、遊間は増加しますので、答えとしては符号を逆にした14.4[mm]です。

 

 

次にレールの温度が55[℃]での応力を求めていきましょう。

熱応力の公式は下のようなものでした。

これを使って熱応力を求めていきましょう。

熱応力σ = -EαΔt

= -206×10³ × 11.5×10^(-6) × (55 – 45)

= -23.7[MPa]

熱応力の符号がマイナスになっているので、熱応力は圧縮応力として作用しているということになります。

では最後に答えとしてまとめましょう。

 

答え

-5[℃]の遊間：14.4[mm]

55[℃]の圧縮応力：23.7[MPa]

 

 

まとめ

今回は熱によって材料が変形する場合の変形量・熱応力についての問題を取り扱いました。

材料が変形するのは外力だけではありません。

温度変化によって体積が変わることによりも変形しました。

 

このように温度変化が発生する箇所にある材料には違った構造計算が必要となりますので、今回取り扱った問題はマスターしておいてくださいね。

今回の記事は以上になります。

最後まで読んでいただき、ありがとうございました。

保存保存