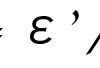今回の記事は、荷重がかかっている材料の伸び・縮み(圧縮量)を求める演習問題を紹介していきます。
この演習問題を解くには、まず材料に荷重がかかっているときのひずみの求め方、また縦ひずみと横ひずみとポアソン比の関係を知っておく必要があります。
それらをまだ理解できていないと、解説を見ずに説くのは難しいですので、まだ理解していない場合は以下の記事を読んでから演習問題に挑戦するようにしてください。
「ひずみの求め方、またひずみとポアソン比についてもうマスターしている!」という人は早速演習問題にトライしてみてください。
今回の演習問題は非常に重要な問題ですので、問題が解けたらしっかりと解答を読み込むようにしてくださいね。
それでは本日も頑張っていきましょう!
演習問題1
直径30[mm]、長さ1[m]の丸棒に50[kN]の引張荷重を与えた。
弾性係数(ヤング率)206[GPa]、ポアソン比を1/3をして、このときの縦方向の伸び、横方向の圧縮量、縦ひずみ、横ひずみを求めなさい。
解答例
まず初めに縦方向の現象について求めましょう。
縦方向の伸びを求めます。
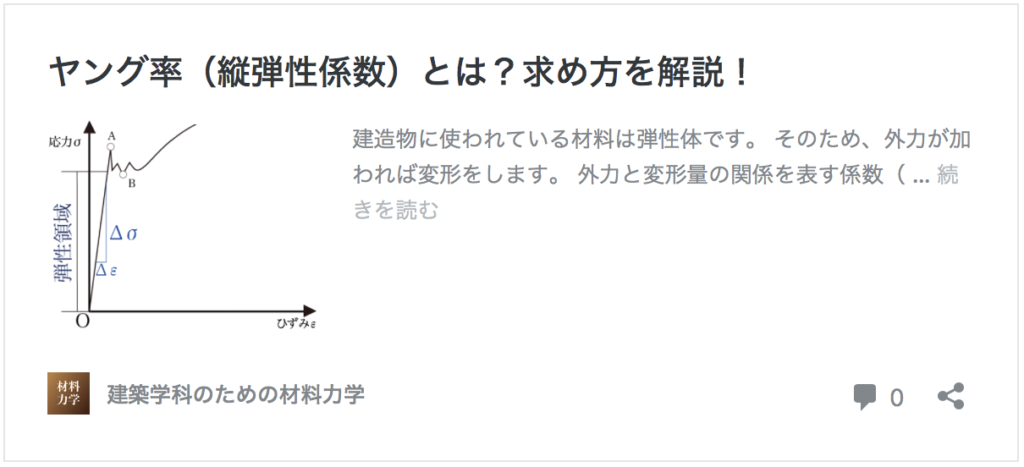
ヤング率(弾性係数)の公式は以下の式でしたね。
ヤング率E = σ / ε
= (P/A) / (λ/l)
= Pl / Aλ
今回はこの公式を変形して、λを求める式にします。
λ = Pl / AE
= 4Pl / πd²E
= (4 × 50×10³ × 1 ×10³) / (π × 30²× 206×10²)
≒ 0.343[mm]
次に縦ひずみを求めましょう。
ひずみの公式は以下のようなものでした。
ε = λ / l
(ε:縦ひずみ、λ:変形量、l:材料の元の長さ)
この公式を使って、縦ひずみを求めます。
変形量λは上で求めた、0.343という値を代入します。
ε = λ / l
= 0.343 / 1×10³
= 3.43×10^(-4)
縦方向の現象について求め終わったので、ポアソン比を用いて横方向の現象を求めます。
ポアソン比の公式は以下で与えられました。
ν = ε’ / ε
(ν:ポアソン比、ε’:横ひずみ、ε:縦ひずみ)
これを変形して用いて、横ひずみを求めます。
問題文でポアソン比は1/3と与えられていましたので、それを用いて横ひずみを求めます。
ε’ = νε
= 1/3 × (3.43×10^(-4))
= 1.14 × 10^(-4)
最後に横方向の圧縮量を求めます。
今回は丸棒に引張荷重が作用してますので、材料の縦方向は伸びます。
材料の縦方向が伸びたので、材料の横方向は縮む(圧縮する)ことになります。
横方向のひずみは以下の式でも求められました。
ε’ = σ / d
(ε’:横ひずみ、σ:荷重の方と垂直な方向の変化量、d:材料の元の横の長さ)
上の公式を用いて圧縮量であるσを求めます。
横ひずみの公式を、σを求める公式に変形して使っていきましょう。
σ = ε’d
= 1.14 × 10^(-4) × 30
= 3.42 × 10^(-3)[mm]
最後にこれらを答えとしてまとめましょう。
答え
縦方向の伸び:0.343[mm]
横方向の圧縮量:3.43 × 10^(-4)
縦ひずみ:1.14 × 10^(-4)
横ひずみ:3.42 × 10^(-3)[mm]
まとめ
今回は材料に引張荷重が作用している場合の材料の縦方向の伸び・ひずみと横方向の圧縮量・ひずみを求めました。
また縦方向の現象について求めてから、ポアソン比を用いて横方向の現象について計算をしましたね。
ポアソン比は縦ひずみと横ひずみの関係を表した割合ですので、ポアソン比が問題で与えられている場合はポアソン比をして縦横の変換をできるということを覚えておきましょう。
今回紹介した演習問題は簡単なものを取り上げましたが、とても重要な問題です。
材料力学を学んでいく上では必須の知識になるので、しっかりとマスターしてくださいね。
今回の記事は以上になります。
最後まで読んでいただき、ありがとうございました。
今後も材料力学の勉強を頑張っていきましょう!!