今回は材料に軸荷重(引張・圧縮)がかかった時に発生する材料伸び・縮みを求める問題を紹介していきます。
材料に引張力がかかったときは材料が伸びますし、圧縮力がかかったときは材料が縮むことはイメージしやすいかと思います。
この形式の問題は、大学の演習課題などでも頻繁に見受けられますので、ぜひマスターしてください。
伸び・縮みを求める演習問題
演習問題1
下の図のような直径20[mm]と直径40[mm]の段付き丸棒に、30[kN]の引張荷重が作用している。
材料のヤング率(縦弾性係数)を206[GPa]として、図の①の部分と②の部分に発生する応力と全体の伸びを求めなさい。

解答例1
まずは考え方から書いていきましょう。
最初に①と②の部分にそれぞれ30[kN]の荷重が均一に作用すると考えます。
①と②の部分に発生する応力をσ1とσ2、伸びをλ1とλ2として計算をしていきます。
では実際に応力を求めていきます。
σ1 = P / A1
= 4P / πd1²
= (4×30×10³) / (π×20²)
= 95.5[MPa]
σ2 = P / A2
= 4P / πd2²
= 4×30×10³ / π×40²
= 23.9[MPa]
次に伸びを求めます。
ヤング率の公式がE = Pl/Aλでしたから、これを変形してλ = Pl/AEの式を使います。
λ1 = Pl1/A1E
= 4Pl1 / πd1²E
= (4×30×10³×500) / (π×20²×206×10³)
= 0.232[mm]
λ2 = Pl2/A2E
= 4Pl2 / πd2²E
= (4×30×10³×300) / (π×40²×206×10³)
= 0.035[mm]
最後に全体の伸びを求めます。
全体の伸びは①と②の伸びの和に等しいので
λ = λ1+λ2
= 0.232 + 0.035
= 0.267[mm]
答え
①の部分の応力:95.5[MPa]
②の部分の応力:23.9[MPa]
全体の伸び:0.267[mm]
この場合、応力の値が近似値(四捨五入した値)となるため、上の算出過程で求めた値と異なる場合もあります。
今回の演習問題では算出値が一致をしています。
E = Pl / Aλ
λ = Pl / AE
σ = P / Aなので、これを上の式に代入して
λ = σ × l/E
λ1 = σ1 × l1/E
= 95.5 × 500/(206 × 10³)
= 0.232[mm]
λ2 = σ2 × l2/E
= 23.9 × 300/(206×10³)
= 0.035[mm]
演習問題2
外形100[mm]、内径60[mm]のパイプと直径60[mm]の丸棒を組み合わせた長さ500[mm]の部材がある。
この両端に変形を無視できる剛体を挟んで、両端に200[kN]の圧縮荷重が作用している。
パイプのヤング率(縦弾性係数)を200[GPa]、丸棒のヤング率を100[GPa]として、それぞれの材料に発生する応力と部材全体の縮み(圧縮量)を求めなさい。
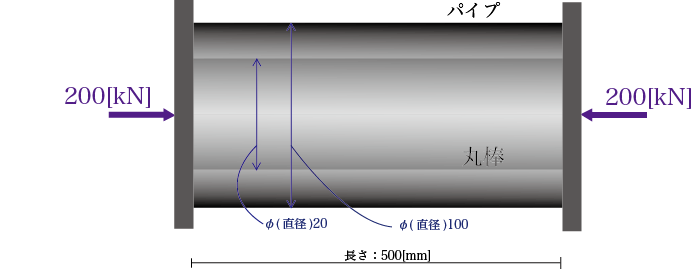
(φ20とは直径20[mm]のことを指します)
解答例2
ではこの問題の解答をみていきましょう。
考え方として、パイプと丸棒に発生する応力は異なりますが、縮み(圧縮量)とひずみは等しくなります。
そのため、圧縮荷重をPとして、パイプと丸棒にかかる荷重とそれぞれP1、P2として計算をしていきます。
最初にパイプと丸棒に発生する応力σ1、σ2を求めていきます。
圧縮荷重のPは、パイプと丸棒にかかる荷重の和と等しいので、P = P1 + P2
応力の公式σ = P / Aから、P = σAとなるので、P = σ1A1 + σ2A2…(1)
圧縮量は等しいことによりひずみも等しいので、ヤング率の公式E = σ / εを変形したε = σ / Eより、σ1/E1 = σ2/E2…(2)
これらの式から応力σ1・σ2を求めます。
(2)の式を変形すると、σ2 = σ1 × E2/E1
これを(1)の式に代入し、σ2を消去すると、
圧縮荷重P = σ1A1 + σ2A2
= σ1A1 + σ1×(E2/E1)× A2
= σ1 × {A1+(E2/E1)×A2}
= σ1 × (A1E1+A2E2)/E1
上のP = σ1 × (A1E1+A2E2)/E1を応力σを求めるための式に変形して
σ1 = P × E1/(A1E1+A2E2)…(3-1)
同様に、σ2 = P × E2/(A1E1+A2E2)…(3-2)
次に圧縮量λを求めます。
ヤング率の公式E = Pl / Aλを変形して、λ = Pl / AE
σ = P/Aより、λ = σ × l/E
上で導いた(3-1)と(3-2)をσ1とσ2に代入して
圧縮量λ = σ1 × l/E1 = σ2 × l/E2
最後に数値を代入して答えを求めます。
式(3-1)と(3-2)で面積を求めるため、d1=φ100、d2=φ60とします。
σ1 = P × E1/(A1E1+A2E2)
= PE1 / {π(d1²-d2²)/4×E1 + πd2²/4×E2}
= PE1 / {π/4×(d1²-d2²)E1 + π/4×d2²E2}
= 4PE1 / π{(d1²-d2²)E1 + d2²E2}
この式に数値を代入して、
σ1 = 4 × (200×10³) × (200×10³) / {π×((100²-60²) × 200×10³ + 60² × 100×10³)}
= 31.1[MPa]
σ2 = σ1 × E2/E1より、
σ2 = (31.1 × 100×10³) / (200×10³)
= 15.6[MPa]
最後にパイプの値を代入して縮み(圧縮量)を求めます。
λ = σ1 × l/E1
= 31.1 × 500 / (200×10³)
= 0.078[mm]
答え
パイプの応力:31.1[MPa]
丸棒の応力:15.6[MPa]
縮み(圧縮量):0.078[mm]
まとめ
今回は引張力と圧縮力がかかった場合の伸び・縮みを求める問題を解きました。
このような問題はよく大学の授業や問題集などでも取り扱われる重要問題ですので、復習をしてマスターするようにしてくださいね。
今回の記事は以上になります。
最後まで読んでいただき、ありがとうございました。

