今回は梁に発生するせん断力を求める問題を紹介していきましょう。
梁に発生するせん断力に関する考え方は、下の記事で紹介しています。
前知識が何もない方は、この記事を読んでから今回の演習問題を解いていくようにしてください。
では早速演習問題を紹介していきます。
実際に紙とペンで手を動かしながら解いていってくださいね。
今回の問題は比較的基礎的な内容です。
演習問題1:1つの集中荷重を受ける両端支持梁
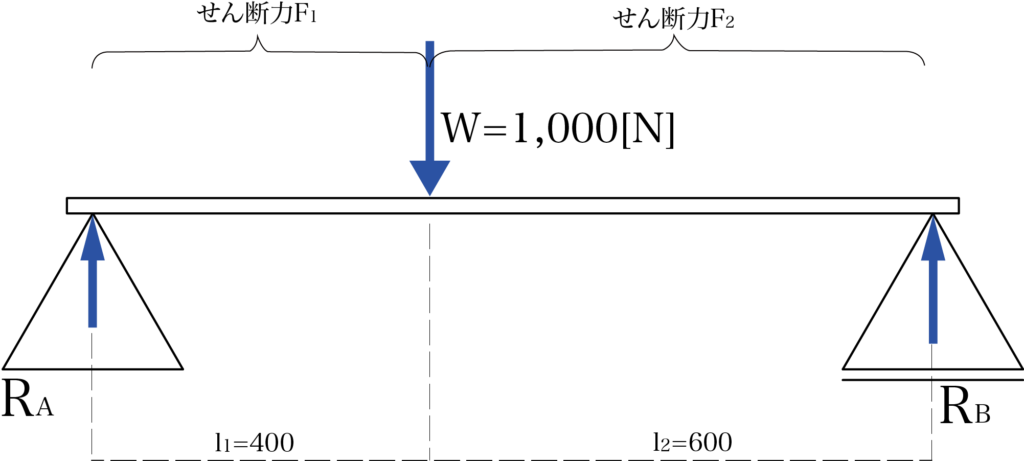
下の図のように、1つの集中荷重を受ける両端支持梁の、荷重の左右に発生するせん断力を求めなさい。
集中荷重Wは1000[N]、支点反力をそれぞれRA・RBとします。
解答例
では解答例を書いていきます。
最初に支点反力のRA・RBを求めていきましょう。
これらの支点反力は高校物理の知識だけでも解くことができますね。
最初にRBから求めていきましょう。
RB = Wl1 / (l1 + l2)
= 1000×400 / (400+600)
=400[N]
RA = W – RB
= 1000 – 400
= 600[N]
支点反力が求まったので、この結果を用いて荷重の左右に発生するせん断力を求めていきます。
左側の支点から荷重点までのせん断力F1は、任意の仮想断面の左側で支点反力RA(=-600)、右側は荷重(=1,000)と支点反力RB(=-400)の和となります。
よって、下の図のようなせん断力が内部に発生していることになります。

{-(-600)[N]↑}は、断面の左側の外力の総和が上向き(-)に600[N]を表しています。
同様に{600[N]↓}は、断面の右側の外力の総和が下向き(+)に600[N]を表しています。
仮想断面x-x’の左側に-をかけて、せん断力の符号を決めています。
F1は+600[N]になります。

F1と同じように考えると、せん断力F2は上のような図になります。
仮想断面の左側の外力の総和に-をかけた値が求めたいせん断力です。
F2は-400[N]です。
答え
F1:+600[N]
F2:-400[N]
ここまで梁の説明で、全般について、下向きの力を+、上向きの力を-と統一しています。
梁のせん断力については、「仮想断面の左側では外力の合計の符号を反転する。右側では外力の合計の符号はそのままにする」として考えてきました。
これは、表現を変えて考えて美雨と、「仮想断面の左側では下向き力を-、上向きの力を+として、右側では下向きの力を+、上向きの力を-として、右側では下向きの力を+、上向きの力を-とする」ということと同じになります。
以上のことを理解することができれば、仮想断面の左右のどちらか外力の数の少ない部材に関して、外力の代数和を計算して、仮想断面左側の外力の合計が上向きのせん断力を+とする、としてせん断力を求めることができます。
梁の問題を解いていくには、多くの手順を必要としますので、過程を理解した上で、より簡単に答えを出せる方法を身につけていきましょう。
まとめ
いかがだったでしょうか。
せん断力は材料力学を勉強する上で欠かすことのできないものですが、その中でも今回は簡単な演習問題を出題しました。
この問題はせん断力を理解する上で基礎となる例題ですので、しっかりとマスターするようにしておいてくださいね。
今回の記事は以上になります。
最後まで読んでいただき、ありがとうございました。