熱応力とは？計算方法は？熱ひずみと弾性ひずみの関係も紹介！

今回の記事では熱応力の概念について解説していきます。

熱応力について勉強する前に、線膨張係数について知っていなければなりません。

 

線膨張係数とは、材料に温度変化が発生し、体積変化が起きた時の材料の軸方向に変化する度合いのことでした。

単位温度あたりのひずみで表したものを線膨張係数αと定義されるのでしたね。

この線膨張係数に関しては、下の記事に詳しくまとめてあるので、まだ知らない人はしっかり確認するようにしておきましょう。

熱ひずみの計算法とは？線膨張係数の計算方法は？

 

さて、では本題の熱応力について解説をしてきましょう。

 

 

熱応力とは？計算方法は？

材料の両端を固定して、熱による自由な変形をしないようにすると、本来の変形量が外力の作用と同じ効果を材料に与えることになり、材料に応力が発生します。

これを熱応力と呼びます。

 

熱応力は、温度変化のある機械や構造体に発生するものです。

固定に応じた量が発生します。

材料が固定されていない場合には材料は自由に変形できてしまうので、熱応力は発生しません。

 

断面積Aの材料の両端を固定して温度変化Δtを与えると、固定された長さの変化ぶんが材料に働く荷重Pとして作用します。

垂直応力σ0と弾性ひずみε0が発生すると考えます。

 

 

イメージを膨らませるために、下の図を見てみましょう。

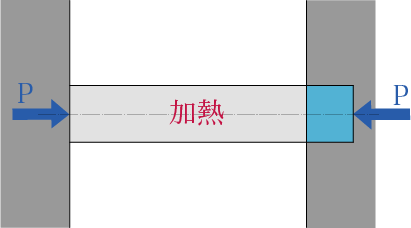
材料を加熱した場合に発生する熱応力について考えて行きます。

材料を加熱すると、材料の体積は膨張しますから、材料水色の部分だけ体積が膨張しようとします。

しかし材料は固定されているので、その体積変化は起きず、その分荷重Pに圧縮されて弾性ひずみが生まれると考えます。

 

 

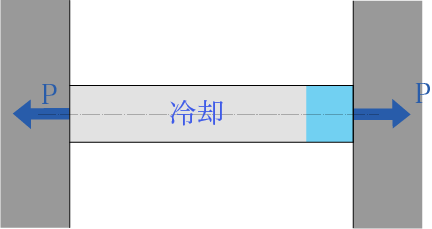
次に材料が冷却された場合です。

材料が冷却されると、体積が減少します。

体積は本来減少されますが材料は固定されていますので、体積の減少分(水色)が荷重Pに伸ばされて男性ひずみが生まれると考えます。

こちらが熱ひずみの中でも材料が冷却されたときの場合です。

 

熱応力の計算方法は？公式は？

材料は固定されているので実際には材料の変形量はゼロですから、材料に発生する熱ひずみεと弾性ひずみε0の輪がゼロとして、材料に発生する熱応力σを次のように考えます。

その計算方法(公式)を紹介していきましょう。

 

熱応力は熱ひずみと弾性ひずみの和から求めることができます。

加熱では、Δtの符号が正(プラス)ですから、熱応力の符号が負(マイナス)になります。

この場合は材料に圧縮応力が発生するということになります。

 

逆に冷却の場合にはΔtの符号が負(マイナス)になり、熱応力の符号は正(プラス)になります。

材料には引張応力が発生します。

 

 

まとめ

今回は熱応力に関して解説しました。

熱応力は材料が固定されていた時にのみ発生する応力です。

材料が固定されていないときは材料が自由に体積変化できてしまうので、熱応力が発生しないことを覚えておきましょう。

 

また、熱応力の公式も紹介しました。

熱応力は加熱の時に符号がマイナス、つまり圧縮応力として発生します。

冷却の場合は符号がプラスになり、引張応力として作用します。

このことについても覚えておきましょう。

 

今回の記事は以上になります。

最後まで読んでいただき、ありがとうございました。