応力集中とは？応力集中係数（形状係数）の求め方も解説！

応力の求め方は、『荷重P / 断面積A』で求められましたね。

しかしこれは荷重を受ける部材の断面形状がどこでも一定として応力を求めています。

そのため、断面形状がどこでも一定でない材料では応力の求め方が変わってくるのです。

 

断面形状の不均一な部材に発生する応力の求め方や、その対策案を紹介していきましょう。

また、記事の後半では、断面形状について詳しく解説をしていきます。

 

 

応力集中とは？対策案は存在する？

では最初に応力集中について書いていきます。

部材に穴や切り抜きなどの断面形状の変化があると、その周辺で圧政する応力が局所的に増大します。

この現象を応力集中と呼びます。

応力集中の度合いは断面形状によって変化しますが、断面形状の変化が著しいほど大きくなります。

 

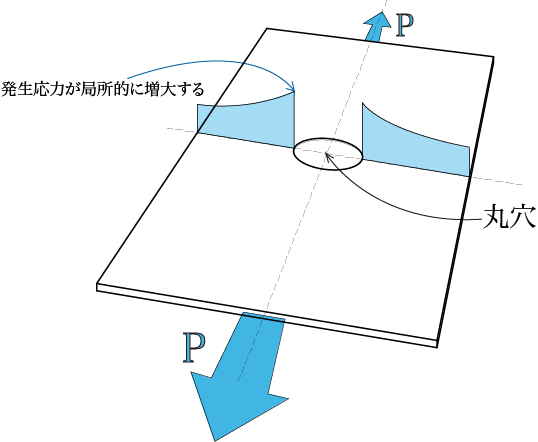
上の図は丸穴のあいた平板に引張荷重が作用した場合の図です。

平板に丸穴が開いていると、材料の軸には図の水色のような応力が発生します。

このように断面形状が一定ではない場合は応力集中が発生するのです。

上の図の場合では、丸穴付近の応力が局所的に増大しています。

 

応力は応力集中が発生せずに材料に均一的に発生していた方が良いので、応力集中はなるべく減らすように検討しなければなりません。

応力集中の対策法としては以下のような方法があります。

• 上のような材料の真ん中に丸穴が開いている場合は、丸穴の半径をなるべく小さくする。
• 材料のコーナー部分へできるだけ大きな円弧、あるいは面取りを設けるようにする。

断面形状によって対策は異なりますが、「応力集中はなるべく起こらないようにする！」ということは覚えておいてください。

 

形状係数の求め方は？円の場合の形状係数はどうなる？

次に形状係数について解説していきましょう。

上では応力集中について解説してきましたが、穴の近傍で局所的に発生する応力を最大応力σmaxとすると、応力集中を考えずに最小断面に一様に分布すると仮定した平均応力σnで、最大応力を割った値を形状係数（応力集中係数）αと呼びます。

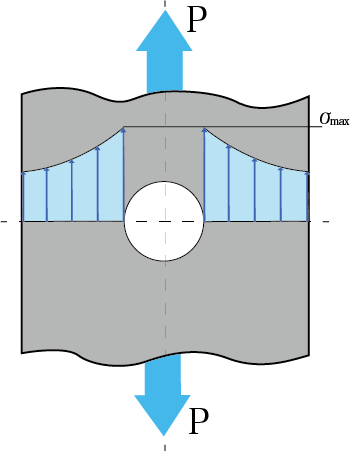
穴の近傍で発生する最大応力σmaxは、応力分布曲線の一番高いところです。

材料に穴が空いている場合の実際の応力集中は上の図のようになります。

 

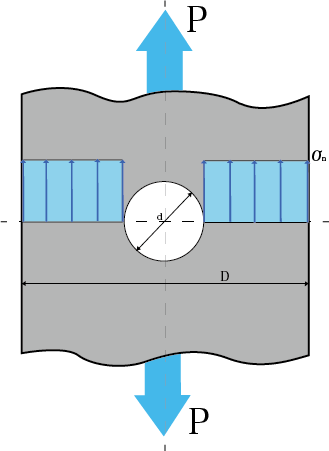
平均応力σnは、応力集中を考えずに最小断面で割った値のことです。

平均応力の式は以下のようになります。

σn = P/(D – d)t

 

 

形状係数（応力集中係数）を公式化すると、以下のようになります。

 

 

まとめ

今回は応力集中についてまとめた記事となりました。

応力集中とは材料の断面形状が均一でないことにより応力が場所によって変化するというものでした。

そして断面形状の変化が著しいほど、応力集中の度合いは増えるということでしたね。

 

また、断面の形状によって応力集中が発生するということでしたが、それを数値化したものが形状係数でした。

この記事では形状係数の公式も紹介しましたね。

最大応力と平均応力についてはしっかりと覚えておきましょう。

 

今回の記事は以上になります。

最後まで読んでいただき、ありがとうございました。