この記事では、伝動軸のねじれと軸の断面の関係を用いてねじり応力とねじれ角を求める例題を紹介していきます。
ねじり応力とねじれ角を求める問題では、伝動軸のような軸のねじれと軸の断面の関係についてを知っていなければなりません。
以下の記事で取り上げていますので、問題の解き方が全く浮かばない場合は参考にしながらとくようにしてください。
さて、では早速例題を紹介していきましょう。
演習問題1:ねじり応力とねじれ角を求める問題
500[rpm]で10[kW]の動力を伝達する長さ500[mm]、直径30[mm]の中実円形軸に発生するねじり応力とねじれ角を求めなさい。
横弾性係数(ヤング率)を80[GPa]とします。
解答例
考え方としては、動力からねじりモーメントであるトルクを求め、ねじり応力τとねじれ角θををそれぞれ計算していきます。
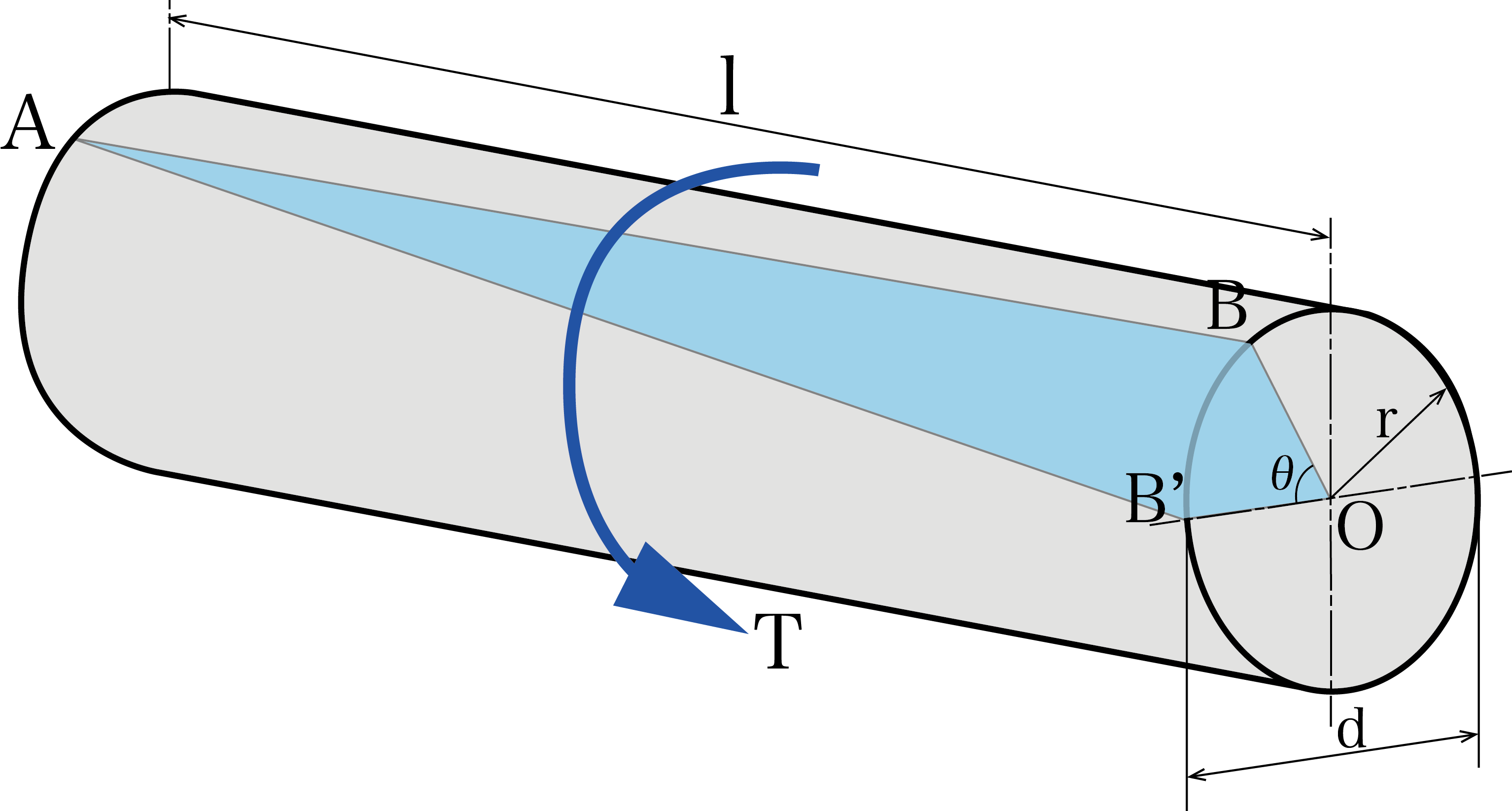
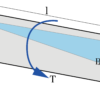
上の画像のような軸があった時、軸の変形を動力と回転数は以下の式で表されました。
T = P×60×10³/2πN
(T:トルク[N・mm]、P:動力(仕事)[W]、N:回転数)
この式を用いてはじめにトルクを求めていきます。
T = P×60×10³/2πN = (10×10³×60×10³)/(2π×500) = 1.91 × 10⁵[N・mm]
次にねじり応力τを求めていきます。
ねじり応力τは以下の式で求めることができます。
τ = 16T/πd³
(τ:ねじり応力[MPa]、T:トルク[N・mm]、d:軸の直径[mm])
上の計算でトルクを求めたので、この値を代入してねじり応力を求めます。
τ = 16T/πd³ = (16×1.91×10⁵)/(π×30³) = 36.0[MPa]
最後にねじれ角のθを求めます。
ねじれ角θは以下の計算で求めることができるのでした。
θ = l/G × 32T/πd⁴
(θ:ねじれ角[rad]、l:軸の長さ[mm]、G:横弾性係数(ヤング率)[MPa]、T:トルク[N・mm]、d:軸の直径[mm])
この式と上の計算で求めてきた、トルクを用いてねじれ角θを求めます。
θ = l/G × 32T/πd⁴ = 500/(80×10³) × (32×1.91×10⁵)/(π×30⁴) = 0.015[rad]
答え
ねじれ応力:36[MPa]
ねじれ角:0.015[rad] = 0.86[°]
演習問題2:軸のこわさを求める問題
軸の長さ1[m]あたりのねじれ角θのことを軸のこわさと呼びます。
軸のこわさは(1/4)[°]よりも小さい値をとるとします。
500[rpm]で10[kW]の動力を伝達する中実円形軸の直径を、こわさ(1/4)[°]として求めなさい。
横弾性係数(ヤング率)を80[GPa]とします。
解答例
もしかすると軸のこわさは初めて聞く単語かもしれません。
軸のこわさは単位長さあたりのねじれ角のことなので、結局はねじれ角に代入すればよいだけです。
難しく考えすぎず、解答例を見ていきましょう。
まず最初にトルクを求めていきます。
トルクの求め方は演習問題1と同様です。
T = P×60×10³/2πN
(T:トルク[N・mm]、P:動力(仕事)[W]、N:回転数)
数値は最後に代入するので、トルクはこの式のまま計算をしていきましょう。
さて、ねじれ角θの式から直径を求める式に変形していきましょう。
θ = l/G × 32T/πd⁴
(θ:ねじれ角[rad]、l:軸の長さ[mm]、G:横弾性係数(ヤング率)[MPa]、T:トルク[N・mm]、d:軸の直径[mm])
∴ d = ∜(l/G × 32T/πθ)
上の式に、ねじれ角θの式を代入してシータを消去します。
d = ∜(l/G × 32T/πθ) = ∜{l/G × 32T/π × 180/θπ}
では数値を代入して、値を出していきましょう。
d = ∜(l/G × 32T/π × 180/θπ)
= ∜{1,000/(80×10³) × (32×1.91×10⁵)/π × 180/(0.25×π)}
= 48.6[mm]
ねじれ角は[rad]の弧度法で計算するので、軸のこわさ(1/4)[°]の度数法を弧度法に変換して代入しています。
答え
軸の直径:48.6[mm]
まとめ
今回は、ねじり応力とねじれ角、またそれらを用いて軸の直径を求める問題を紹介しました。
高校物理も公式を覚えて計算で使えるようになるまで練習をしていた人も多いと思いますが、基本的に大学の物理の分野の勉強方法も同様のやり方が一番効率よく理解をしていくことができます。
なんども復習をして理解を深めていってくださいね。
今回の記事は以上になります。
最後まで読んでいただき、ありがとうございました。