ねじり応力と軸径(直径)を求める計算演習例題

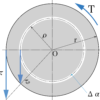
今回の記事では、ねじりモーメントを受ける材料のねじり応力・軸径を求める計算演習例題を紹介していきます。

『軸径』という単語を普段見ない人が多いと思いますので、軸径について最初に軽く触れていきましょう。

軸径とは軸の寸法のことです。

材料力学で用いる軸径は、直径のことを指します。

 

さて、軸径とは何かについて軽く説明が終わったところで、問題を見ていきます。

ねじりモーメントを受ける軸の寸法は、極断面係数を使って求めます。

極断面係数に関しては、以前の記事にまとめてありますので、まだ理解が進んでいない方はその記事を読んでから今回の問題を解いていきましょう。

 

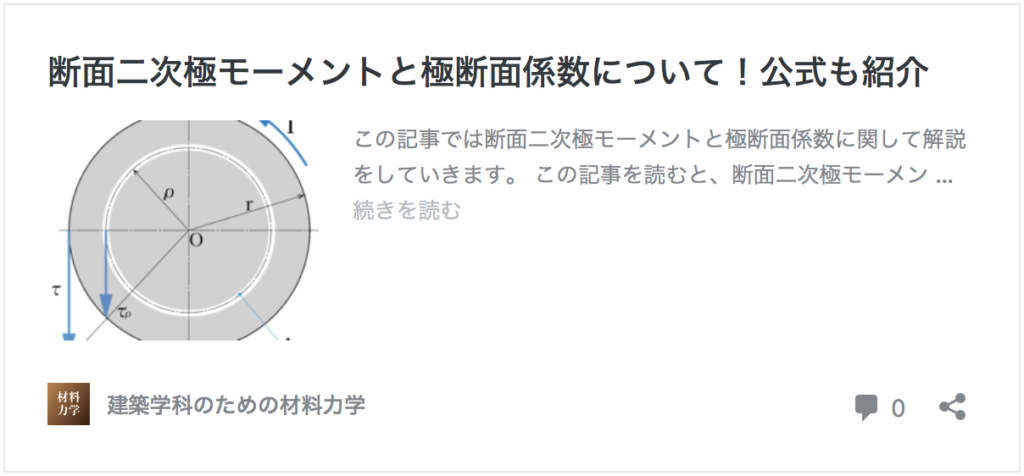
では早速問題に入っていきます。

 

 

演習問題1：ねじり応力を求める計算問題

直径50[mm]の軸に、1.5×10⁶[N・mm]のねじりモーメントが作用している。

このとき発生するねじり応力を求めなさい。

 

 

解答例

では早速解答例を見ていきます。

こちらは公式から数値を代入するだけでもとまる問題なので、公式を覚えている人にとっては簡単な問題かもしれません。

ねじり応力は以下の式で求めることができましたね。

この公式に当てはめて求めていきます。

また、中実軸(空洞がない軸)の極断面係数は、以下のようなものでした。

Zp = π/16 × d³

この式と上で紹介した公式を組み合わせて、ねじり応力を求めます。

 

T = τZpとZp = π/16 × d³から、T = τ × π/16 × d³

∴τ = 16T/πd³

この式に問題で与えられた数値を代入していきます。

τ = 16T/πd³  = (16 × 1.5×10⁶) / (π × 50³) = 61.1[MPa]

 

答え

ねじり応力τ：61.1[MPa]

 

演習問題2：軸径を求める計算問題

2 × 10⁶[N・mm]のねじりモーメントが加わる中実円形軸の許容ねじり応力を50[MPa]とする。

このときの軸径である直径を求めなさい。

 

 

解答例

この問題は演習問題1が解けた人にとっては簡単な問題かもしれません。

演習問題1で導出した式を用いて解いていきましょう。

 

演習問題1から、τ = 16T/πd³

∴d = ∛(16T/πτ) = ∛{(16 × 2×10⁶)/(π × 50)} = 58.8[mm]

 

答え

軸径：58.8[mm]

 

 

演習問題3：

内径60[mm]、厚さ10%の中空円形軸(空洞のある円形軸)と等しいねじり強さを持つ中実円形軸の直径と、2つの軸の重量比を求めなさい。

 

 

解答例

では解答に入っていきます。

これは少し応用した問題ですが、このような問題もよく問われますので、ぜひマスターしていきましょう。

 

中空軸の外径をd2とすると、d2 = 1.2d1 = 1.2 × 60 = 72[mm]

 

中空円形軸の極断面係数は以下の式で与えられました。

中空円形軸の極断面係数ZP = π/16 × (d1⁴ – d2⁴)/d2⁴

この公式を使います。

 

ねじり強さが等しいので、2つの軸の極断面係数が等しくなります。

よって、π/16 × d³ = π/16 × (d2⁴ – d1⁴)/d2

両辺にπ/16をかけて、

d³ = (d2⁴ – d1⁴)/d2

∴d = ∛{(d2⁴ – d1⁴)/d2} = ∛{(72⁴-60⁴)/72} = 57.8[mm]

 

次に重量比を求めていきます。

重量火は面積比と等しくなりますので、最初に2つの軸の断面積を求めていきます。

中実軸の断面積A1 = π/4 × d²

中空軸の断面積A2 = π/4 × (d2² – d1²)

 

よって、

A1/A2 = d²/(d2² – d1²) = 57.8²/(72² – 60²) = 2.1

これらをまとめて答えとしていきましょう。

 

答え

中実軸の直径：57.8[mm]

重量比：中軸軸の重量が中空軸の2.1倍

 

 

まとめ

今回はねじりモーメントを受ける軸のねじり応力や軸径などの寸法を求める演習問題を紹介しました。

基本的な問題が多かったので、公式を暗記している人にとっては簡単な問題だったかもしれません。

しかしこのような基礎問題の理解は非常に大切ですので、ぜひ何度も復習して理解を深め、今後の勉強に役立てていってくださいね。

 

今回の記事は以上になります。

最後まで読んでいただき、ありがとうございました。