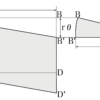
この記事では、ねじれ応力・ねじれ角・せん断角などの軸の変形の計算演習例題を扱っていきます。
演習問題を重ねながら、ねじれ応力・ねじれ角・せん断角などの軸の変形の計算に慣れていきましょう。
それでは早速問題を見ていきましょう。
目次
演習問題1:ねじり応力の計算例題
ねじり荷重を受ける丸棒に、0.001のせん断ひずみが生じている。
この時、ねじり応力を求めなさい。
横弾性係数を80[GPa]とします。
解答例
では解答を見ていきます。
この問題は簡単なので、暗記していく勢いでやっていきましょう。
横弾性係数の公式は以下のようなものでした。
G = τ / γ
(G:横弾性係数、τ:ねじり応力(せん断応力)、γ:せん断ひずみ)
弾性係数=応力/ひずみの関係を覚えておくと、この公式も暗記しやすくなるのではないでしょうか。
この公式にそれぞれの値を代入して、ねじり応力を求めていきます。
G = τ / γ
∴ねじり応力τ = Gγ = 80×10³ × 0.001 = 80[MPa]
答え
ねじり応力:80[MPa]
演習問題2:せん断ひずみとねじり角の計算例題
長さ1[m]、直径30[mm]の丸棒に、40[MPa]のねじり応力が生じている。
せん断ひずみとねじれ角を求めなさい。
横弾性係数を80[GPa]とします。
解答例
では解答例を見ていきます。
こちらも基本的に公式に当てはめて計算するだけなので、公式を覚えてしまっている人には簡単な問題かもしれません。
演習問題1でも紹介したように、横弾性係数の公式は以下のようなものでしたね。
G = τ / γ
(G:横弾性係数、τ:ねじり応力(せん断応力)、γ:せん断ひずみ)
まずはこの公式に当てはめて、せん断ひずみを求めていきましょう。
G = τ / γ
∴せん断ひずみγ = τ / G = 40 / 80×10³ = 5 × 10^(-4)
次にねじれ角を求めていきます。
ねじれ角は以下の公式から得られました。
γ = rθ/l
(γ:せん断ひずみ、r:半径、θ:ねじれ角、l:丸棒の長さ)
この公式を変形して、ねじれ角を求める式にします。
γ = rθ/l
∴ねじれ角θ = rγ / l
ここで、rは半径であることに注意して、値を代入して計算していきます。
また、単位は[mm]に合わせて計算するので、丸棒の長さは1,000[mm]として代入します。
∴ねじれ角θ = rγ / l = 1,000 × 5×10^(-4) / (30/2) = 0.033[rad]
これらの計算結果をまとめて答えを出していきましょう。
答え
せん断ひずみ:5 × 10^(-4)
ねじり応力:0.033[rad]
角度の単位の変換
角度の単位の変換について補足をしておきましょう。
円の中心角360[°]は、360[°]=2π[rad]
つまり、180[°]=π[rad]です。
1[°]=π/180なので、x[°]の時の[rad]は以下のようになります。
θ = x × π/180 [rad]
演習問題3:直径を求める計算例題
ねじり荷重を受ける長さ1[m]の丸棒で、最大ねじれ角2[°]、許容ねじり応力60[MPa]としたい。
このとき、必要な直径を求めなさい。
横弾性係数を80[GPa]とします。
解答例
では解答を見ていきます。
この演習問題3は、少しばかり応用問題となっています。
演習問題1と演習問題2で扱った公式を合わせて答えを求めていきます。
G = τ / γ (G:横弾性係数、τ:ねじり応力(せん断応力)、γ:せん断ひずみ)
γ = rθ / l = dθ / 2l (γ:せん断ひずみ、r:半径、θ:ねじれ角、l:丸棒の長さ、d:直径)
dθ / 2l = τ / G → d = 2l/θ × τ/G
最大ねじれ角の2[°]を[rad]に変換します。
θ = 2 × π/180
これらの数値を代入して、答えを求めていきましょう。
d = (180 × 2 × l)/2π × τ/G = (180 × 2 × 1,000 × 60) / (2 × π × 80 × 10³)
= 43.0[mm]
答え
直径:43.0[mm]
演習問題4:
直径40[mm]の軸がねじられて、ねじれ角1.5[°]、ねじり応力35[MPa]が発生した。
軸の長さとせん断角を求めなさい。
横弾性係数を80[MPa]とする。
解答例
では解答を見ていきます。
τ = Gγ = G × rθ/l = Gdθ/2l
よって、l = Gdθ/2τ
1.5[°]を[rad]に変換します。
θ = 1.5 × π/180
軸の長さl = Gdθ/2τ = (80×10³ × 40 × 1.5 × π) / (2 × 35 × 180) = 1,197[mm]
せん断角φ = γ = rθ/l = dθ/2l = (40 × 1.5 × π) / (2 × 1,197 × 180) = 4.4×10^(-4)
これらをまとめて答えとしていきます。
答え
軸の長さl = 1,197[mm]
せん断角φ = 4.4×10^(-4)
まとめ
今回はねじり応力・ねじれ角・せん断角などの変形に関する問題を紹介しました。
この記事で取り上げた問題に関しては、公式を覚えていれば解ける問題が多かったのではないでしょうか。
ぜひ復習を何度もして、理解を深めていってくださいね。
今回の記事は以上になります。
最後まで読んでいただき、ありがとうございました。