今回のこの記事では、集中荷重と分布荷重について解説をしていきます。荷重の概念やその種類については下の記事で紹介しています。
材料力学では外力を荷重と呼ぶ!内力の仮想断面の考え方や作用・反作用の法則について
せん断荷重、軸荷重とは?せん断力と軸力とはどう違う?違いを説明
こちらの記事では荷重について扱ってきましたが、その荷重をさらに広げた考え方をしてみましょう。
高校の力学などでは、一点に働く荷重を考えてきました。主に力は一点に働くものを想定し、問題に解いていたと思います。しかし材料に作用する荷重には、狭い範囲に働く荷重の他にも広い範囲に働く荷重も存在します。
例えば手のひらで壁を押すときのことを考えてみましょう。高校の授業などでは手のひらで壁を押した場合にも、力は一点に働くものと考えたはずです。実際には手のひらは面積があるものなので、一点に働くことは実世界ではあり得ないのです。
このような面積を持つものや、長さを持って分布する荷重の接し方から荷重を分類していきましょう。
集中荷重とは?今まで扱ってきた力のほとんどが集中荷重だった!
集中荷重とは、矢印線の視点や矢の先端で一点に働くように表す荷重です。文字だけでは分かりづらいと思うので、図を見て考えてみましょう。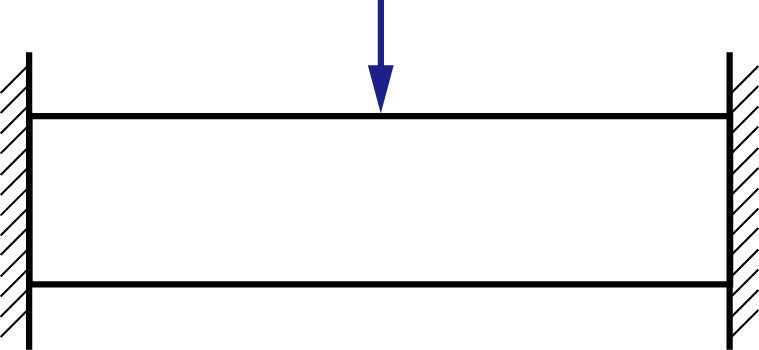
点は厳密位に配置だけを表して面積をもちません。面積をもたないので、圧力のように面積で割って力を考える必要がないです。
しかし実際には、画鋲のような尖った先端の点に力を集中するだけでなく、その多くの場合が床に置いた物体のように材料とは面で接触しています。このような場合でも、計算を簡単にできるようにするため、集中荷重(力が点に集中した荷重)として扱い考えることができます。こちらが今まで私たちが主に問題を解くときに考えてきた『力』という概念です。
分布荷重とはどんなもの?
では次に集中荷重とは違う、分布荷重というものを考えてみましょう。板に持った土のように、広い接触面をもつ荷重のことを分布荷重と呼びます。このような場合だと、土の盛り方が均一でない限り、板に与える荷重の大きさは場所によって異なります。土が高く盛られているところほど荷重の大きさが大きくなります。分布荷重は、図で表すと下のようになります。
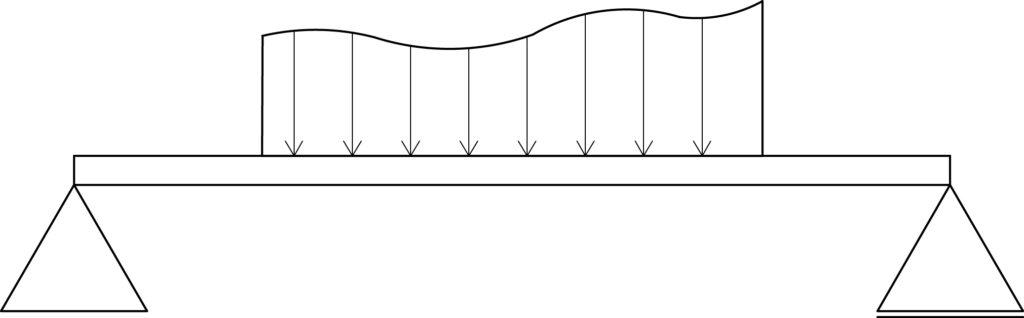
上記のような場合で、材料に対して均一に荷重が分布するものは、等分布荷重と呼ばれます。簡略化した図を用いると、等分布荷重は下のように表します。
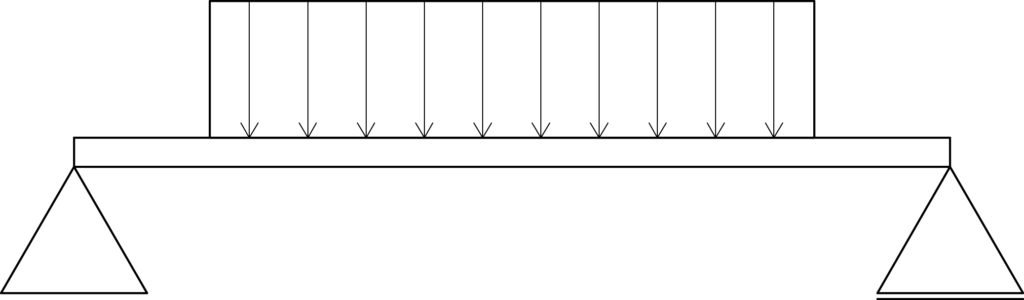
等分布荷重は材料力学の問題を解いていくに当たってよく出てきますので、その概念をしっかり理解するようにしておきましょう。
自動車のように移動するものは移動荷重と呼ぶ!
では自動車を例にとって考えてみましょう。
自動車ですが、タイヤから荷重が作用してそれが移動するという性質があります。例えば橋の設計などをする際にはこういったことを考慮する必要がありますが、自動車から作用する荷重は一点に働く力ではありませんね。
走行中の自動車が路面に与える重量はほぼ一定です。このような重量の変わらない自動車のような移動する荷重を移動荷重と呼びます。
高度な構造計算をするような場合は移動荷重が出てくることがあるかもしれませんが、この力を考慮することはあまりありません。「そういえば移動する荷重もあるんだよなぁ」程度に覚えておいてください。
材料自体もそのほとんどが荷重になる
最後に材料そのものも荷重になることを確認して終わりましょう。高架の高速道路や長大橋などの大型構造物では、丈夫なものでなければならないので、十分な強度が必要とされます。
丈夫にしたいからといって構造体の材料自体の重量が大きくなると、材料自体の分布荷重を考慮する必要がでてきます。確かに強度は大切ですが、構造体の材料自体の重量が大きいて、それだけ柱なども丈夫にしなければなりません。結果として設計費がかさんでしまうということにもなってもしまうので、強度はあるけれでもなるべく費用がかさまない様にすることも重要です。最近では強くて軽い材料なども開発されてきています。
まとめ
今回は荷重の分布についてまとめました。
今まで主に扱っていた集中荷重。こちらは概念の理解や計算を簡単にするために使ったものでした。
次に取り扱ったのは分布荷重についてでした。等分布荷重は荷重の大きさが等しく分布したものでしたね。
この集中荷重と等分布荷重については今後の問題でもよくでてきますので、しっかりと理解をしておきましょう。
今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。
