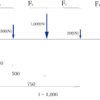
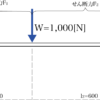
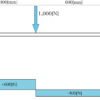
今回は肩持ち梁に荷重が複数個作用している場合のせん断力の計算方法を紹介していきましょう。
肩持ち梁は両端支持梁とは違い、支点が一つしかない梁のことです。
支点がひとつしかないため、支点反力も一つだけになります。
両端支持梁のせん断力を求める問題については、以前の記事でまとめていますので、そちらを参照してください。
下の記事は両端支持梁に1つの集中荷重が作用する場合の演習問題です。
こちらの記事は、両端支持梁に複数の集中荷重が作用している場合の演習問題になります。
今回紹介するのは肩持ち梁のせん断力計算問題ですが、両端支持梁とは少し解き方が異なるので、ぜひマスターしてくださいね。
演習問題:複数の集中荷重を受ける肩持ち梁
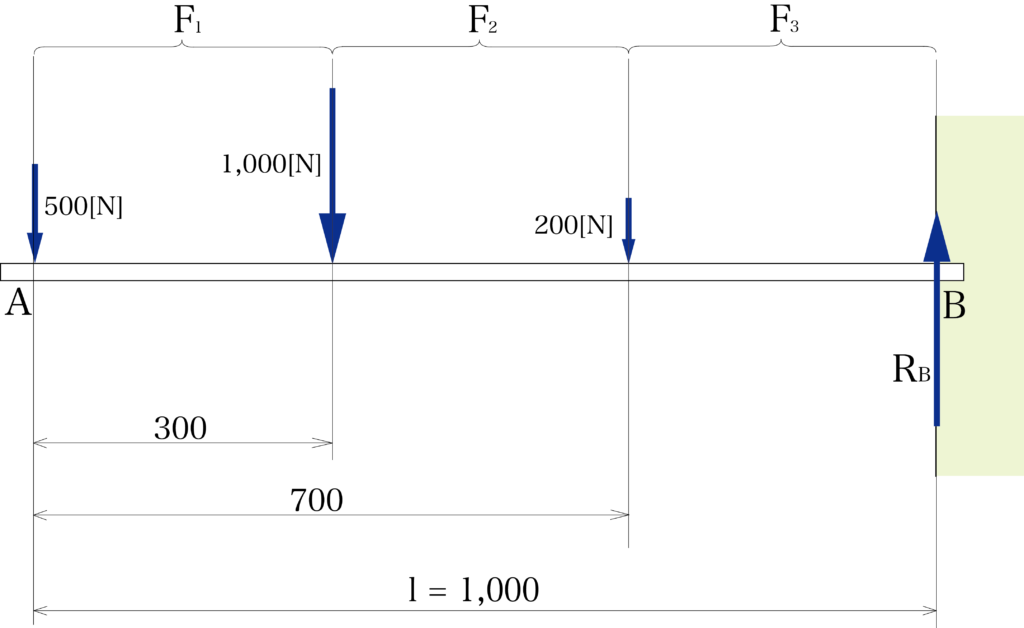
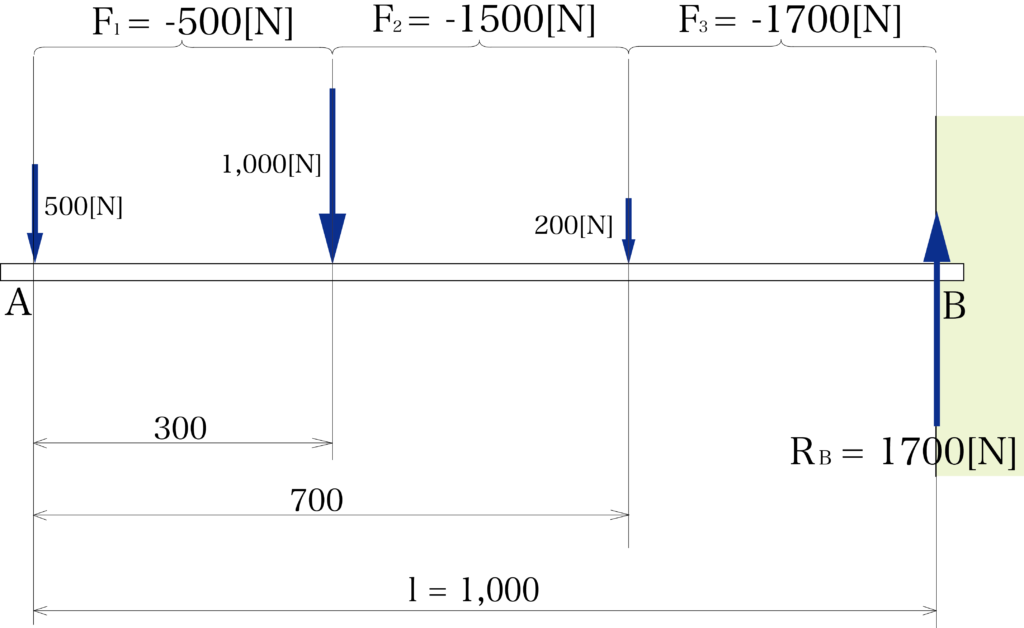
肩持ち梁に上の図のような荷重が作用している時、支点Bの支点反力RBと、それぞれの荷重の左右に発生するせん断力F1・F2・F3を求めなさい。
解答例
では解答に入っていきましょう。
問題を解くときは図を描きながら、計算して出てきた値を図に書き込みながら答えを求めていきましょう。
肩持ち梁の固定されている端点を固定端、他方の固定されていない端点を自由端と呼びます。
肩持ち梁では固定端がすべての荷重を支え、荷重の総和が支点反力になります。
上の問題の図のように、3つの集中荷重が作用すれば、梁は3区間に分けられて、3つのせん断力が発生すると考えられます。
固定端を右に取ると、どの区間でも断面の左側が下向きで右向きが上向きになります。
よってすべてのせん断力の符号は負になります。
ではそれぞれの値の計算に入っていきましょう。
RB = 500 + 1000 + 200 = 1700[N]
支点反力は1つだけなので、すべての荷重の大きさを足したものが支点反力の大きさになります。
では次にせん断力を求めていきましょう。
せん断力F1
-(500)[N] | -500[N]
真ん中の縦棒は仮想断面を示しています。
仮想断面の左側は、A点の荷重である500[N]にマイナスをかけたものです。
仮想断面右側は、1000+200-1700=-500[N]です。
せん断力F2
-(1500)[N] | -1500[N]
仮想断面の左側は、500+1000=1500[N]にマイナスをかけた値。
仮想断面右側は、1000+200-1700=-500[N]です。
せん断力F3
-(1700)[N] | -1700[N]
仮想断面の左側は、500+1000+200=1700[N]にマイナスをかけた値。
仮想断面右側は、支点反力RBの値です。
ではこれらの値を図に書き入れて、答えをまとめましょう。
答え
RB = 1700[N]
F1 = -500[N]
F2 = -1500[N]
F3 = -1700[N]
ここまで梁の説明で、全般について、下向きの力を+、上向きの力を-と統一しています。
梁のせん断力については、「仮想断面の左側では外力の合計の符号を反転する。右側では外力の合計の符号はそのままにする」として考えてきました。
これは、表現を変えて考えて美雨と、「仮想断面の左側では下向き力を-、上向きの力を+として、右側では下向きの力を+、上向きの力を-として、右側では下向きの力を+、上向きの力を-とする」ということと同じになります。
以上のことを理解することができれば、仮想断面の左右のどちらか外力の数の少ない部材に関して、外力の代数和を計算して、仮想断面左側の外力の合計が上向きのせん断力を+とする、としてせん断力を求めることができます。
梁の問題を解いていくには、多くの手順を必要としますので、過程を理解した上で、より簡単に答えを出せる方法を身につけていきましょう。
まとめ
今回は肩持ち梁に複数個の荷重が作用する場合のせん断力の求め方について紹介しました。
せん断力の計算にはまず支点反力を求めるところから始まります。
支点反力がわかると、あとは仮想断面を移動させて言って、流れでせん断力を計算していくことが可能です。
考え方を理解して、問題に慣れていってくださいね。
また、せん断力を考えるときは、せん断力図をかけるようになるとより理解が深まります。
せん断力図の書き方の基本に関しては、以下の図で解説しているのでぜひ見てみてください。
今回の記事は以上になります。
最後まで読んでいただき、ありがとうございました。