今回は断面係数の演習問題を練習していきましょう。
断面係数の求め方については材料力学を学ぶ上で欠かせないものです。
この記事では断面係数を求める基本的な問題をマスターしましょう。
演習問題1:縦長断面が強い理由
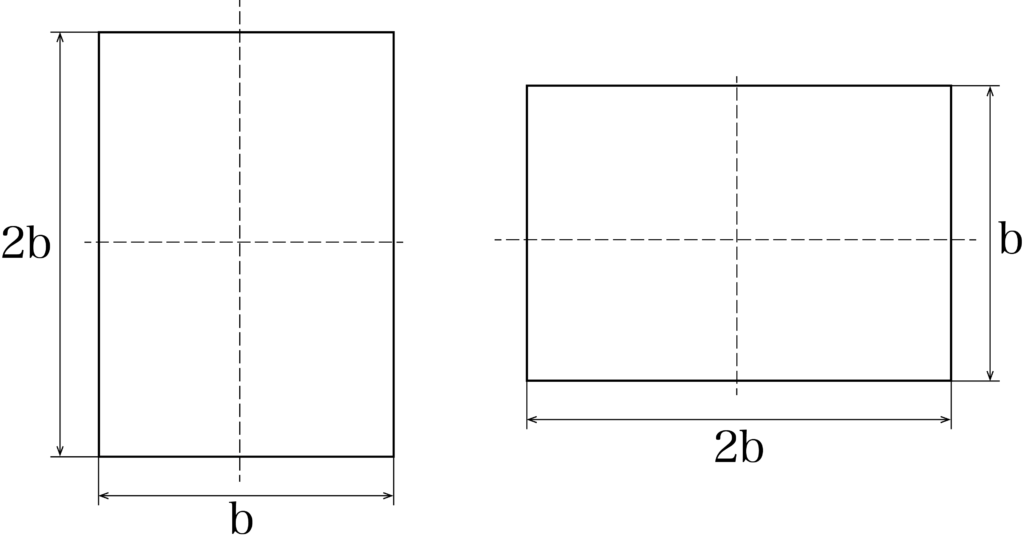
上のような辺の長さの比が1:2の長方形断面がある。
上2つの断面の断面係数をそれぞれ求めなさい。
また、それぞれの断面係数から縦長断面と横長断面ではどっちが強度があるかを比較し、説明しなさい。
解答例
上の図の左側の断面をZ1、右側の断面をZ2として、それぞれの断面係数を計算していきましょう。
長方形の断面係数は以下の公式で求められましたね。
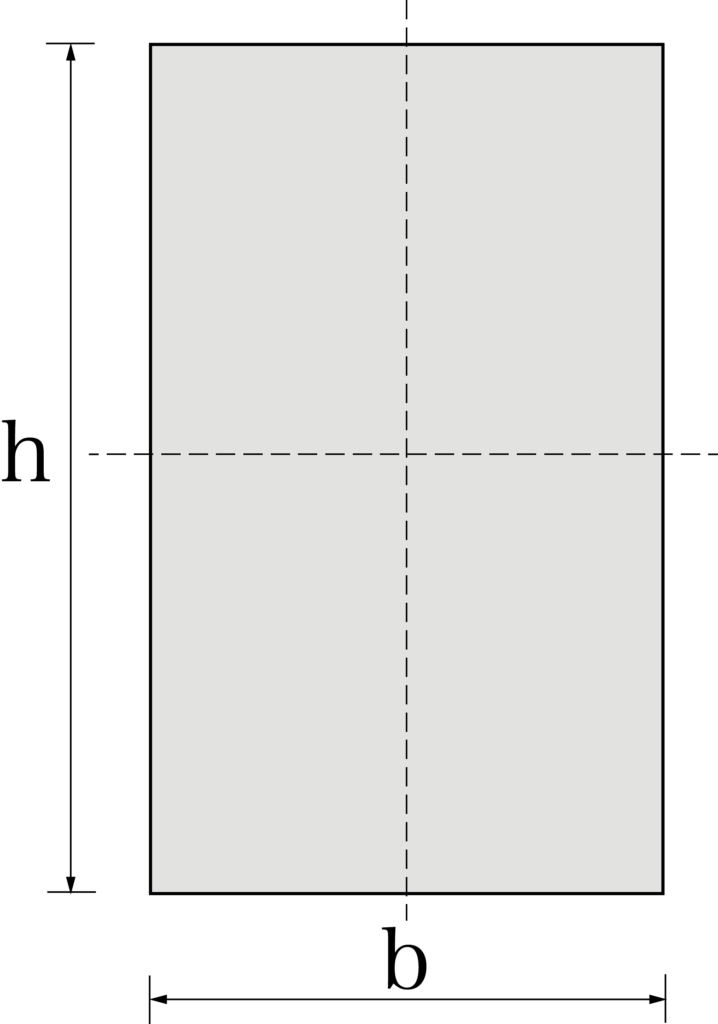
bh²/6
(h:断面の縦の長さ、b:断面の横の長さ)
この公式を用いて断面係数を求めていきます。
Z1 = b(2b)²/6 = 2b³/3
Z2 = 2b×b²/6 = b³/3
それぞれの断面係数が求められたところで、比を出してみましょう。
Z1:Z2 = 2b³/3:b³/3 = 2:1
さて、Z1とZ2の比がでたところで、ここで断面係数の意味について考えます。
梁が強いとは、一定の曲げモーメントMに対して、発生する曲げ応力σが小さいこととします。
曲げ応力の公式は以下のようなものでした。
σ = M/Z
(σ:曲げ応力、M:曲げモーメント、Z:断面係数)
この公式から、曲げモーメントMが一定の時、曲げ応力σの大きさは断面係数に反比例することがわかります。
よって、同じ断面積でも、断面係数が大きい方が強い断面であることがわかります。
縦長断面の断面係数Z1:横長断面の断面係数Z2 = 2:1でしたから、縦長断面に発生する応力は、横長断面の1/2となり、結果として強い断面ということがわかります。
以上のことを踏まえ、解答としてまとめていきましょう。
答え
縦長断面の断面係数Z1:2b³/3
横長断面の断面係数Z2:b³/3
縦長と横長の断面係数の比較とその説明:断面係数は縦長が横長の2倍なので、発生する曲げ応力が1/2になり、結果的に強い断面となる。
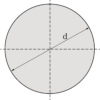
演習問題2:中実丸棒とパイプの比較
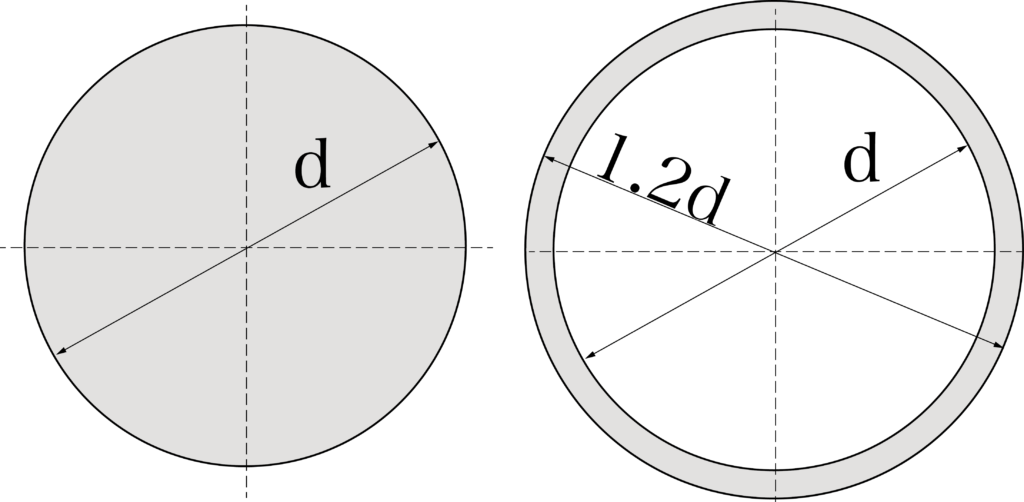
上の図のような直径dと、内径d外径1.2dの薄肉パイプの断面係数がある。
それぞれの断面係数を求めなさい。
解答例
では解答例を書いていきます。
こちらも演習問題1と同様に、丸棒(図の右側)の断面係数をZ1、パイプ(図の左側)の断面係数をZ2としてそれぞれを求めていきましょう。
まず初めに丸棒の断面係数を計算します。
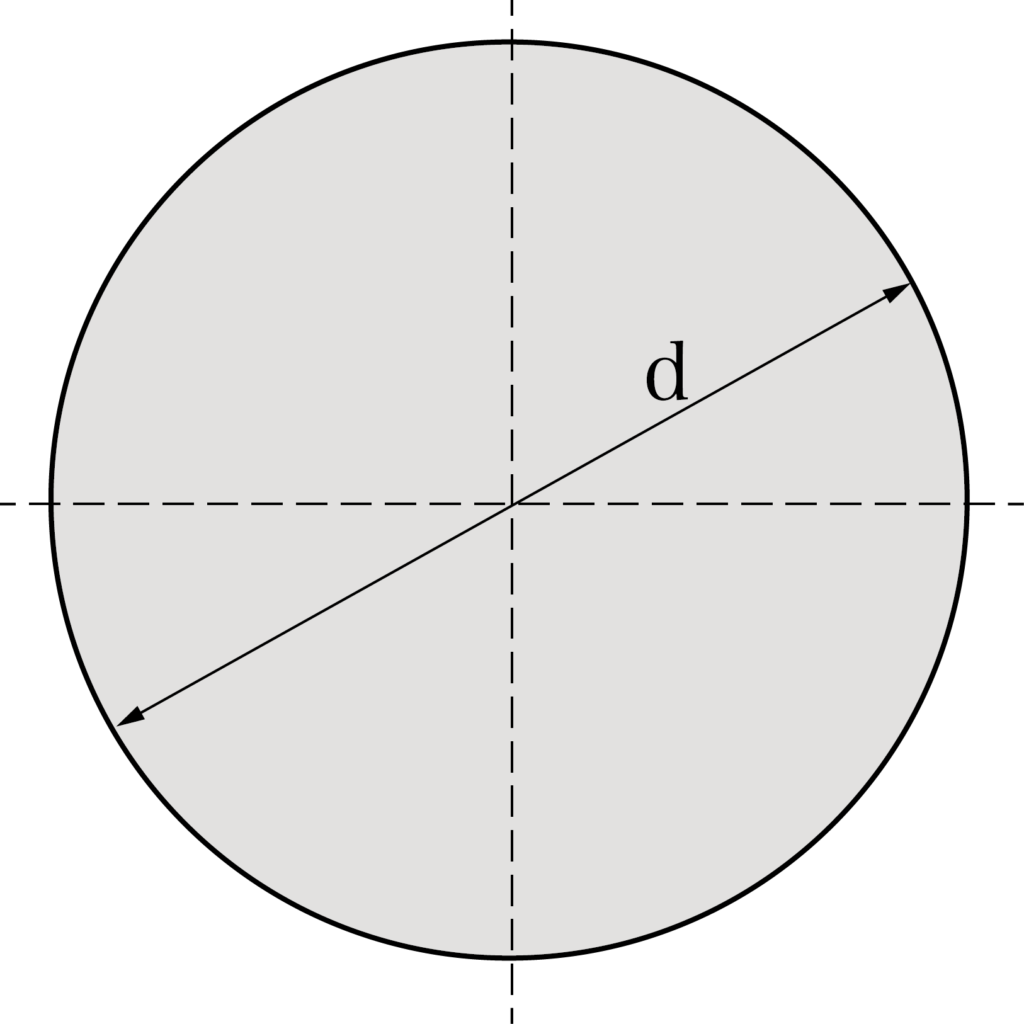
πd³/32
(d:丸棒の直径)
今回問題で与えられた丸棒の直径は公式と同じdなので、公式の値が断面係数の値になります。
よって、
Z1 = πd³/32
次にパイプの断面係数を計算します。
パイプの断面係数は以下の公式で求められます。
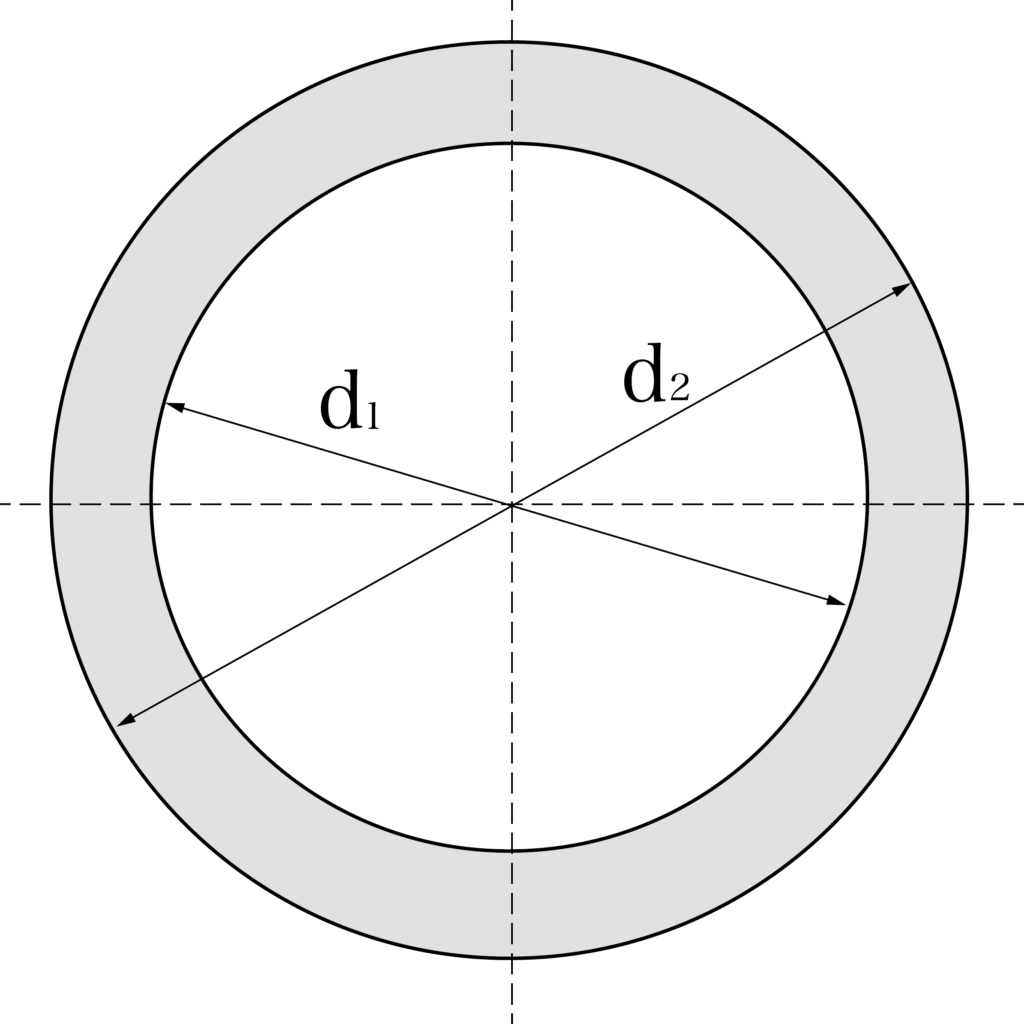
π(d2⁴-d1⁴)/32d2
(d1:パイプの内径、d2:パイプの外径)
上の公式ではパイプの内径をd1、パイプの外径をd2としています。
この演習問題では、
d1 = d
d2 = 1.2d
として当てはめて計算していきましょう。
Z2 = π(d2⁴-d1⁴)/32d2
= π{(1.2d)⁴-d⁴}/32×1.2d
= o.44πd⁴/33.4d
= o.22πd³/16.7
答え
丸棒の断面係数Z1:πd³/32
パイプの断面係数Z2:o.22πd³/16.7
丸棒とパイプの断面係数を比較して比を出してみます。
Z1:Z2 = πd³/32:o.22πd³/16.7 ≒ 1:0.89
この式から、パイプは丸棒の約90%の曲げ強さを持つということになります。
また、丸棒とパイプのそれぞれの断面積を計算してみましょう。
丸棒の断面積をA1、パイプの断面積をA2とします。
A1 = πd²/4
A2 =π(d2²-d1²)/4 = π{(1.2d)²-d²}/4
2つの断面積の比を出すと、
A1:A2 =πd²/4:π{(1.2d)²-d²}/4 ≒ 1:0.44
断面係数の比と断面積の比からわかることは、パイプは丸棒の約45%の面積しか持たないのにも関わらず、曲げ強さを丸棒の約90%も持つということです。
まとめ
今回は断面係数の求め方について勉強しました。
また、演習問題1では同じ断面積を持つ長方形断面を縦長で使う場合と横長で使う場合の強さについても勉強しましたね。
この問題から同じ断面積では、縦長断面で使う方が強度が増すことがわかったと思います。
演習問題2では、丸棒とパイプの断面係数の算出方法について紹介しました。
この問題では、パイプは丸棒の約45%の断面積しかもたないのにも関わらず、約90%もの強度を誇るのでしたね。
今回の記事を参考にしながら、断面係数の算出方法と、断面係数そのものが持つ意味について知識が深まったことかと思います。
是非参考にしながら今後の勉強に役立ててくださいね。
今回の記事は以上になります。
最後まで読んでいただき、ありがとうございました。