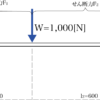
固定支点とローラー支点(移動支点)をもつ両端支持梁に荷重が作用しているときに発生するせん断力について紹介していきましょう。
荷重と支点反力は、梁に対して垂直に作用する外力です。
せん断力はこれらの外力によって、梁の内部に発生します。
ハサミはせん断力を利用して紙を切ることができます。
物体に外力を作用させでズレを起こすことによって紙をせん断します。
これと同じ原理が梁にも発生します。
今回は梁に働くせん断力についてまとめていきます。
両端支持梁に働くせん断力の大きさと向きはどうなる?
高校物理では、力学の分野で力を取り扱うときに、計算をして数値を出して向きは図で考えることが多いと思います。
材料力学でもその考え方でいきましょう。
集中荷重1つを受ける両端支持梁の水平方向右向きをプラスとして、左側の支点Aから、プラス方向に支点Bまで移動する『仮想断面x-x’』を考えていきましょう。
下向きの力をプラスとして、荷重+W、支点反力-RA、-RBとします。
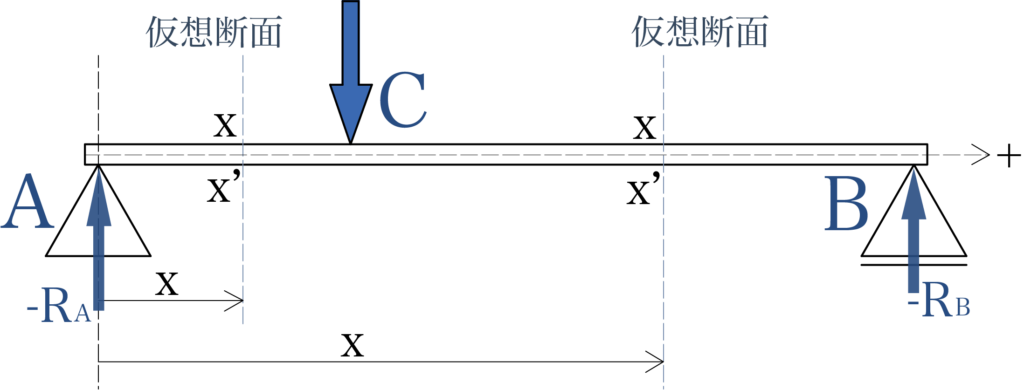
『断面x-x’』で仮想切断した左右の部材ごとに、力の釣り合いを考えます。
集中荷重1つを受ける両端支持梁では、図のように荷重点Cの左側のせん断力FACの大きさはRA、荷重点Cの右側のせん断力FCBの大きさはRBになります。
ここで、仮想断面をつなげて船団力FACとFABを観察すると、2つのせん断力の組み合わせの向きが逆になっていることがわかります。
せん断力の大きさは、図のように力の釣り合いから求めることができますが、組み合わせの向きの違いを示す符号は現れません。
そのため高校物理と同様に、力の向きに関しては図を書いてそこから考えるようにしましょう。
先ほどの図をもう一度見てみましょう。

これは仮想断面を基準に右向きを正とした座標軸を考えています。
そして、断面の左側の内力に「-」をかけて符号を反転してみます。
すると、-FACはFACとなり、FABは-FABとなり符号が逆転します。
この規則性を利用して、断面の左側が上向きで右側が下向きのせん断力の組み合わせを正のせん断力、その逆を負のせん断力と決めます。
せん断力の符号の考え方は?
さて、上では力の数値の大きさを向きについて説明してきました。
仮想断面の左側の外力の合計が上向きで、右側の外力の合計が下向きになるときのせん断力をプラスとして、逆になる場合をマイナスとする符号が一般的に使用されています。
イメージとしては、外力の合計が時計回りの時はプラス、反時計回りの時はマイナスです。
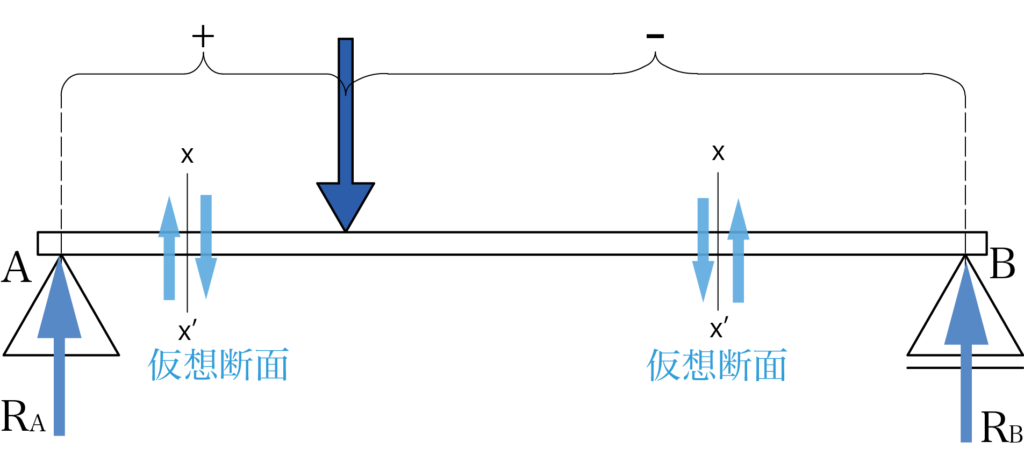
仮想断面の左側が上向きで右側が下向きの力おの組み合わせを+としています。
外力に挟まれた区間で、せん断力の符号と大きさは一定です。
せん断力の符号は時計回りか反時計回りかで考えましたが、せん断力とはズレを与える力のことです。
せん断力を示す矢印を見てみると、互いに逆向きになるので材料を回転させるように見えるかもしれません。
しかし針は支点に支えられて、移動も回転もすることはありません。
そのため、せん断力はズレだけを与えるということを覚えて起きてくださいね。
まとめ
今回は梁に発生するせん断力についてまとめました。
梁には常にせん断力が働いているので、せん断力の理解は非常重要になってきます。
今回の記事を参考にしながら理解を深めていってくださいね。
今回の記事は以上になります。
最後まで読んでいただき、ありがとうございました。