今回は梁の計算方法について紹介していきます。
梁の問題は、最初に支点反力を求めるところから始まります。
支点反力は力の釣り合いと力のモーメントの釣り合いの2つを利用して求めます。
それでは早速内容に入っていきましょう。
両端支持梁の支点反力を求める例題!
最初に下の図を見ていきましょう。
今回はこの図でのはりの支点反力を求めていきます。
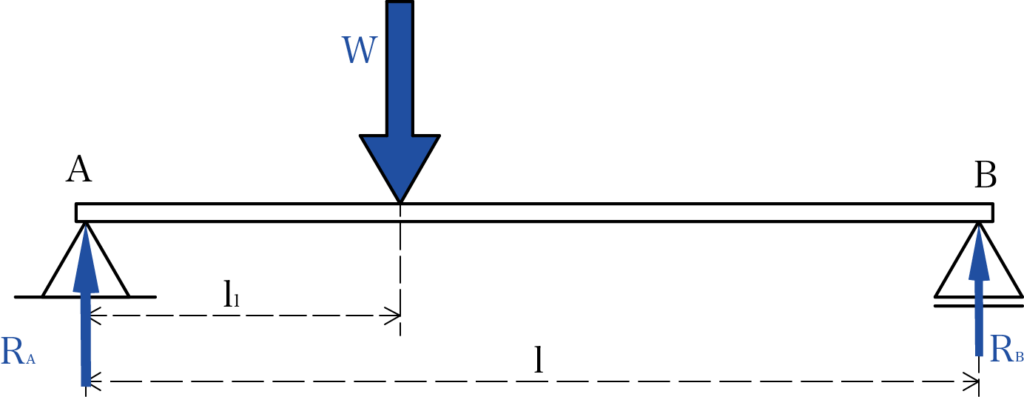
支店間の距離はスパンと呼びます。
スパンl、支点Aからの距離l1の点に集中荷重Wが作用する両端支持梁の支点反力RAとRBを求めます。
梁の静止条件は?
梁が静止するとは、変形しても移動も回転もしないということです。
梁が移動をしない条件とは、梁に作用する鉛直下向きの荷重と、鉛直上向きの支点反力の合計がゼロ、つまりは力の総和がゼロということになります。
荷重と支点班力は、梁を回転させようとする力のモーメントを生みます。
梁が回転しないということは、梁に働く力のモーメントの総和がゼロということになります。
両端支持梁の支点反力の計算方法
力の総和がゼロ、力のモーメントの総和がゼロ、という2つの条件から、支点反力を求めます。
ここでは、下向きの力を+、反時計回りのモーメントを+として、支点Aをモーメントの基準として考えていきます。
では先ほどの図をもう一度見てみましょう。

この図をもとに順を追って支点反力を求めていきます。
①力の総和がゼロから
-(RA + RB) + W = 0
下向きを+としたので、上向きの支点反力は-です。
上むきの力と下向きの力を足すとゼロになる式をたてます。
上の式から、
RA + RB = W…(1)
力の総和がゼロということは、上むきの班力と下向きの荷重が釣り合うということです。
②支点Aを基準として力のモーメントの総和がゼロなので、
RA0 – Wl1 + RBl = 0
基準が支点Aなので、支点班力RAの腕の長さがゼロになり、モーメントを1つ消すことができるようになります。
-Wl1 + RBl = 0…(2)
モーメントが時計回りか反時計回りかで符号が変わります。
③式(2)から支点Bの反力RBを求める。
RBl = Wl1
RB = Wl1/l…(3)
④式(1)に式(3)を代入し、支点Aの反力RAを求めます。
RA = W – RB
= W(l – l1)/l
まとめ
今回は梁の支点反力の求め方の例題を紹介しました。
支点反力は高校物理の知識だけでも求めることができます。
そのため、この例題はそこまで難しくなかったのではないでしょうか。
梁の問題は支点反力を求めるところから始まります。
そのため、簡単ですが今回の例題が基礎となってきます。
しっかりと理解するようにしておいてくださいね。
