今回は梁の基本的な問題の解き方について紹介していきましょう。
梁の問題は求める事象が多いので順を追って考えていく必要があります。
しかし基本的には高校物理の力学の分野をしっかり理解していれば解けることが多いので、基本をしっかり理解していくようにしていきましょう。
力の釣り合いとモーメントの釣り合いがポイントになってきます。
梁の支点反力の求め方は?
今回は両端支持梁での支点反力の求め方について説明をしていきます。

両端支持梁の固定支点と移動支点(ローラー支点)は基礎に支えられています。
基礎とは建築物を支え、地盤に定着させる部分のことです。
下の写真を見てみましょう。

画像出典:http://oka-ken.jp/works/sintiku/
この白いコンクリートを基礎と呼びます。
そして梁に外力として荷重が作用すると、荷重は支点を介して基礎で受け止められます。
基礎は荷重の反作用として、荷重と反対の向きに反力を視点から梁に与えます。
高校物理でいう垂直抗力です。
支点に生じる反力を支点反力と呼び、梁にとっては外力となります。
下の図を見てみましょう。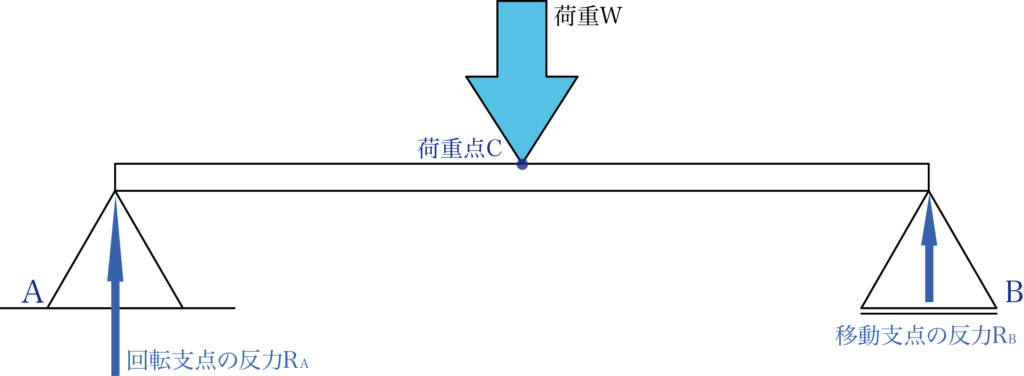
この図では支点反力RAと支点反力RBの我が荷重Wと釣り合って梁は静止していきます。
上の場合、荷重と反力が釣り合う場合は次の式が成り立ちます。
RA + RB = W
これは高校物理でも頻繁に出てくるような釣り合いの式ですね。
回転支点と移動支点の組み合わせをすることによって、梁の変形を拘束しない静定梁ができます。
梁に荷重が働いたときはせん断力が作用する?
次にせん断力についてです。
せん断力は材料力学のような大学の物理で初めて登場する概念ですね。
荷重と支点反力の外力を受けながら静止状態を保っている梁では、全ての任意の仮想断面の左右に、同じ大きさで平行逆向きの内力が生まれます。
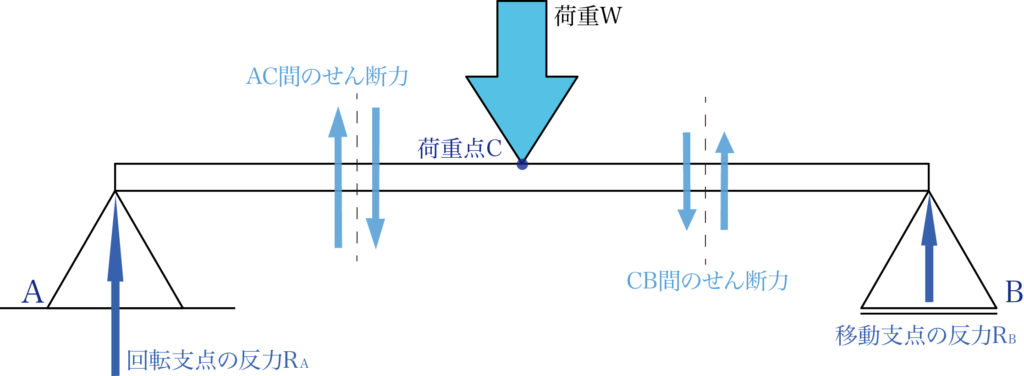
上の図のように、仮想断面の左右に生まれる内力は材料をせん断しようとするので、梁の内部にはせん断力が発生します。
荷重と支点反力が外力として働き、梁の内部にせん断力が生まれるのです。
荷重が大きくなく、それに応じて支点反力が小さい場合は梁はその形をとどめます。
しかし荷重が大きくなり反力が大きくなるとせん断力が大きくなり、梁が専断されてしまうことがあるということを覚えておきましょう。
梁に働く曲げモーメントはどんなもの?
梁に作用する外力(荷重)は、梁を回転させようとする力のモーメントを生み出します。
梁の内部では、すべての任意の仮想断面で反作用として逆向きのモーメントが発生します。
梁の内部に生まれるモーメントは、梁が回転しないように静止させると同時に、梁を曲げるように働くので曲げモーメントと呼びます。
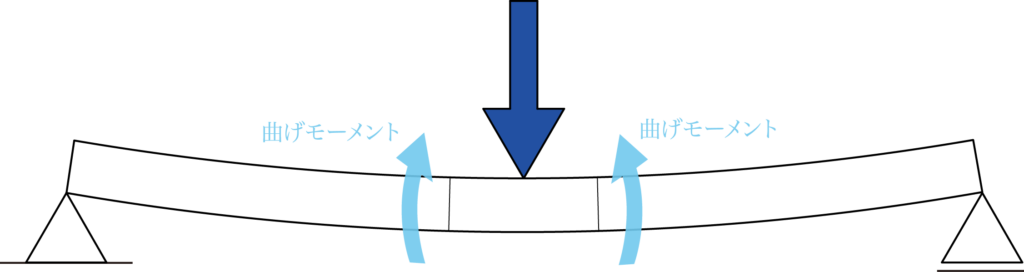
このように、材料には曲げモーメントが発生します。
このとき、支点の曲げモーメントはゼロになります。
内部に生まれるモーメントは、梁の回転を止めますが、梁を曲げるような作用をします。
まとめ
今回は梁について紹介しました。
梁とは柱の上に架け渡される部材のことですが、梁には屋根などの荷重がかかります。
それがどれくらいなのか、また構造物を安全なものにするためにも梁の理解と計算はできるようになっていないといけません。
今回は梁に作用する反力はせん断力、曲げモーメントについて説明をしましたが、この記事の内容はとても重要となりますのでしっかりと理解するようにしてくださいね。
今回の記事は以上になります。
最後まで読んでいただき、ありがとうございました。

