トルクとは？モーメントとの違いは？ねじりモーメントがトルク？

中空材とは中が空洞の材料でしたが、この材料は曲げ荷重やねじり荷重に有効な材料です。

今回は材料に曲げやねじりを与える力とはどんなものなのかを考えていきましょう。

 

 

そもそもモーメントとはどんなものだったか復習

その前に高校物理で勉強してきたモーメントとはどんなものだったのかをおさらいしておきましょう。

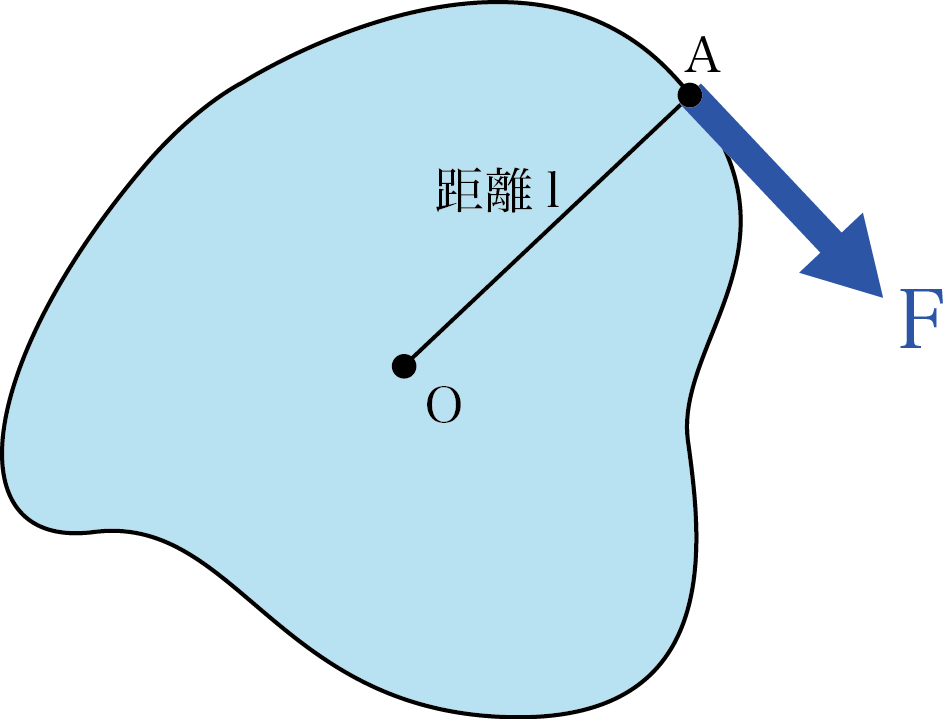
板の点Oを釘で打ち付けて、点Oから距離lにある点Aに、直線OAと垂直な作用線を持つ力Fを作用させます。

Fは点Oを中心として板を回転させる能力をもっています。

この物体を回転させる能力のことをモーメントと呼びました。

力のモーメントの大きさは、力Fの大きさと距離l（作用線までの距離、腕の長さと呼ぶ）の積で表します。

 

モーメントとは回転される能力のことを指すので、力が受けた物体が実際に回転や変形をしていない場合にもモーメントは発生しています。

曲げ荷重は材料を曲げようとする曲げモーメントが発生します。

ねじり荷重の場合は材料をねじろうとするねじりモーメントが発生します。

これらは名前が異なっていますが、どれもモーメントであり材料を変形しようとするものと捉えてください。

 

さて、高校物理で勉強をする力のモーメントについて復習した後で、本題に入っていきしょう。

 

トルクとは？モーメントの違いは？

トルクという単語は高校物理では出てきません。

物理などの自然科学を扱う分野ではトルクは使われることは少ないですが、いま僕たちの勉強している材料力学のような機械工学ではこの単語が登場します。

 

機械工学では、自転車のペダル漕ぎのような軸と力に関するねじりモーメントのことをトルクと呼んでいます。

つまり、トルクとは軸と力に関するモーメントのことを言い換えたものということになります。

 

ペダルを取り付けている腕の役割をする部材はクランクと呼びますが、チェーンと噛み合わせた歯車をスプロケットと呼びます。

クランクはスプロケットを回転させる軸に取り付けられています。

 

脚力が力Fとなり、これとクランクの腕の長さlとの積で生まれるモーメントがトルクです。

このトルクM1と半径rのスプロケットがチェーンに与える力F’との積で生まれるトルクM2が等しいため、大きな力F’が生まれるわけです。

 

 

トルクと馬力の関係（豆知識）

さて、トルクについては以上で説明を終わりますが、ここからは豆知識を書いていきます。

興味のない方はスキップしてもらって構いません。

 

トルクと馬力の話は自動車雑誌等々によく出てきます。

この両者の理解は感覚的に難しいものですが、ここではわかりやすいように簡略化して説明していきます。

 

トルクは自転車のペダルのような仕組みに利用されていました。

トルクが大きいということは、自転車ではペダルを押す力が強いということを意味します。

 

次に馬力についてです。

トルクとはあくまでも瞬間的な力です（ペダルをグッと踏むのも瞬間的）。

そのためトルクを発生させる力を持続することによって、どの程度仕事を行えるのかを表すために考えられた指標が馬力です。

鉄腕アトムでも100万馬力なんて言い方しますよね。

 

もう少し正確にいうと、ある程度決められた時間内に、どれだけ重い荷物をどれだけ遠くまで運べるかを、馬何頭分にあたるかで表示をしたものが馬力なのです。

 

自転車の場合、ペダルを踏む力（クランクの長さは一定なのでトルクの大きさと等しい）に、ペダルの回転数を掛け合わせると馬力を求めることができます。

トルク × 回転数 = 馬力

それでは、自転車でペダルを踏んでなおかつ一生懸命回すとどうなるのでしょうか。

それはもちろんスピードが上がり、移動距離も伸びます。

もし自転車に荷物を乗せていたとすると、人がかつづよりも短時間で遠くに運ぶことができます。

このどれだけ仕事をしたかの指標が馬力というわけです。

 

馬力が材料力学で使われることはあまりありませんが、「馬力ってそういうことなのかぁ」程度に知っておくと良いかもしれませんね。

 

 

まとめ

今回は高校物理のモーメントの復習から、トルクとはどんなものであるかを説明しました。

トルクとは自転車のペダルのような軸と力のねじりモーメントの言い換えなのでしたね。

高校物理で扱った自然科学ではこのような単語は使われまっせんでしたが、材料力学のような機械工学では使われる単語であるということを覚えておいてください。

 

今回の記事は以上になります。

最後まで読んでいただき、ありがとうございました。