この問題では中実円形柱と中空円形柱の座屈応力と座屈荷重を求める計算問題を紹介していきます。中実円と中空円ではどのように座屈応力と座屈荷重の値が変化するのかを、比較しながら説明をしていきます。
座屈荷重や座屈荷重を求めるためにはオイラーの式、ランキンの式を使いますが、その式を使うためには断面二次半径を求める必要があります。中実円と中空円の断面二次半径の求め方やその比較に関しては、以前まとめた記事がありますので、そちらを参照してからこの計算問題を読んでいただけると一層理解が深まると思います。また、座屈応力や座屈荷重を求める手順に関しても以前解説した記事があります。ぜひ活用してください。
では早速内容に入っていきましょう。
目次
演習問題:中実・中空円柱の座屈応力・荷重を求める問題
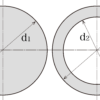
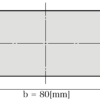
長さ2[m]の軟鋼製で、両端を固定した柱があります。下の図の2つの柱について、それぞれの座屈応力と座屈荷重を求めなさい。また、その結果を比較して得られる考察をしなさい、縦弾性係数(ヤング率)を206[GPa]とします。
解答手順
では解答例を見ていきます。まずはじめに上の2つの柱の座屈応力と座屈荷重を求めるために断面二次半径kを計算していきましょう。
断面二次半径kを求める
最初に2つの柱の断面二次半径を求めていきます。断面二次半径kは断面二次モーメントIを断面積Aで割った値の平方根をとったものです。中実円の断面二次半径をks(sは’solid’のsです)、中空円の断面二次半径をke(eは’empty’のeです)として計算していきましょう。まずは中実円の断面二次半径からです。
Is = πd⁴/64、As = π(d/2)²より、
ks = √(Is/As) = √(πd⁴/64 × 4/πd²) = √(d²/14) = d/4
値(d=60[mm])はまだ代入せず、文字のまま進めていきましょう。
次に中空円の断面二次半径です。外径をd2、内径をd1として計算します。
Ie = π(d2⁴-d1⁴)/64、Ae = π(d2²- d1²)/2²より、
ke = √(Ie/Ae) = √{π(d2⁴-d1⁴)/64 × 2²/π(d2²- d1²)}
= √{(d2⁴+d1⁴)(d2²- d1²)/16(d2²- d1²)} = √(d2²+d1²)/4
細長比λと求める
中実円と中空円の断面二次半径が求まったので、その値を使って細長比を求めます。細長比λは柱の長さl(=2,000[mm])を断面二次半径kで割った値です。
λs = l/ks = 4l/d = 4×2,000/60 = 133
λe = l/ke = 4l/√(d2²+d1²) = 4×2,000/√(60²+40²) = 111
細長比は”比”なので、単位はありません。
座屈計算の計算式を決定する
次に座屈計算の計算式を決定します。座屈計算は、長柱の場合はオイラーの式、中間柱の場合はランキンの式で計算します。今回の問題の柱は軟鋼製ですので、λ<90√nを満たしていれば中間柱で計算式はランキンの式になります。そうでない場合(λ>90√n)の場合は、長柱でありオイラーの式で座屈計算します。
この条件式を検証するために端末係数nを考えます。問題は「柱の両端は回転支持」と書いてありますので、n=1となります。よって、90√n=90となります。
中実円の細長比λs=133、中空円の細長比λe=111、ですので、これらはどちらも90よりも大きい(λ>90√nが成り立つ)ので、これらの柱は長柱として扱いオイラーの式で座屈計算をしていきます。
座屈応力σを計算する
では座屈応力を求めていきましょう。座屈計算はオイラーの式でしていくことが上でわかったので、オイラーの式の座屈応力の計算式を確認しましょう。
σ = n × π²E/λ²
(σ:座屈応力[MPa]、n:端末係数、E:縦弾性係数(ヤング率)[GPa]、λ:細長比)
では中実円と中空円の座屈応力を計算しましょう。今回の問題の縦弾性係数(ヤング率)は206[GPa]なので、206×10³[MPa]として代入します。
中実円の座屈応力σs = n × π²E/λs² = 1×π²×206×10³/133² = 115.0[MPa]
中空円の座屈応力σe = n × π²E/λe² = 1×π²×206×10³/111² = 165.0[MPa]
求めた答えから、中実円よりも中空円の方が応力が大きくなることがわかります。これは、単に断面積が中空円の方が小さいからと考えると、納得がいくのではないでしょうか。
しかし、中空円の方が座屈応力が大きいからといって、大きな荷重をかけることが可能かというと、そういうわけではありません。これは、下の座屈荷重を計算して検証して見ましょう。
座屈荷重Pを計算する
最後に座屈荷重を計算をしましょう。荷重は応力に断面積をかけることで求めることができます。上で求めた座屈応力にそれぞれの断面積をかけて、座屈荷重を求めていきましょう。
中実円の座屈荷重Ps = σs×As = σs×πd²/4
= 115×π×60²/4 = 325×10³[N]
中空円の座屈荷重Pe = σe×Ae = σe×π(d2²-d1²)/4
= 115×π×(60²-40²)/4 = 259×10³[N]
上で求めた座屈荷重の値から、座屈荷重は中実円の方が中空円より大きくなっています。座屈応力の値は中空円の方が大きかったのですが、座屈荷重では大小関係がひっくり返っています。これは、荷重が応力に断面積をかけて求めるためです。
今回の問題では、中空円よりも中実円の方が断面積が大きいため、このような結果となっています。
答え
中実円の座屈応力:115.0[MPa]、中空円の座屈応力:165.0[MPa]
中実円の座屈荷重:325×10³[N]、中空円の座屈荷重:259×10³[N]
考察:座屈応力は中空円の方が大きくなり、座屈荷重は中実円の方が大きくなる。
まとめ
今回は中実円と中空円それぞれの座屈応力と座屈荷重を求める問題を紹介しました。座屈計算と中実・中空円の比較を複合した問題でした。
材料力学では、このように2つの材料を実際に計算しながら比較する問題が出題されることがあります。今回のような問題に慣れておけば、大学の試験でもしっかり考察ができるようになると思います。ぜひ復習をして、理解を深めていってください。
今回の記事は以上になります。最後まで読んでいただき、ありがとうございました。